---------------------------------------------------------------
---------------------------------------------------------------
Infinite division of congruent similarities
There are essentially two terms that pertain to the Greek concept of "wholeness" denoted by the prefix "holo." Holography refers to two-dimensional coordinate mapping, such as onto a piece of paper or film. Holography allows us to view an image from multiple perspectives, as well as being able to retain the entire image in any piece of the film paper that is cut off into a smaller piece. The other currently known of form is the hologram, or three-dimensional image capture rendering in real space and time, and not using any filmic or flat medium.
Essentially, my theory on these, apparently only two, forms of "wholeness" rendering is that holography is like the flat shape of a two-dimensional fractal image. There are many different types of two-dimensional or flat fractal sets, ranging from the Julia to the Mandelbrot to the Cantor and Menger. However what all of these have in common is that their central shape, their strange "attractor" (to borrow a term from chaos theory) is interiorly non-reducable. The centre on the inside of any fractal pattern is a place of infinite replication known as the Feigenbaum scaling function, whereby any finite number of smaller or larger segments can cover the "attractor" of the logistic map. In order to depict these "strange attractors" in three space, they have to be rotated and stretched such that measure a 3D slice of a 4D Quaternion fractal set as it is rotated (that is what renders an attractor "strange"). Here is a depiction of such a quarter twisted "strange attractor" extracted from the "dark space" of a two-dimensional fractal:
-source: http://commons.wikimedia.org/wiki/Image:QuaternionJuliaWP.png
So, essentially, you can think of a holograph as a flat, two-dimensional image, such as the standard Mandelbrot or Julia sets of fractals, and you can associate the term hologram with a three-dimensional rendering of a quaternion rotation of the fractal set's strange attractor. Here are a brief example of each to demonstrate the essential difference:
 /
/ 
the moving image on the left is a fractal. The "magic eye" image on the right is a 3-d rendering of a "strange attractor."
Now, I postulate their to be a third type of "implicit wholeness" theorem that can be geometrically depicted. In the same way that the holograph is the fractal edge and the hologram the strange attractor interior, so too are there a special set of fractals based on transcendental and transfinite iterations. These occur only when very certain, specific numbers are slected to form the angle and and iteration ratios that determine the edging pattern of the fractal. For example, when the number of repititions of angle replication is set to phi (1.618), then the clear pattern of a fibonnaci sequence or "Golden" spiral will appear. Another form of regularly cycling fractal pattern is based on the square root of two (the diaganol of a square with legs of one and area of one squared); we see this pattern occurs in the branching patterns of plants.
 \
\ 
On the left we see the branching pattern of the square root of two mimicked on a computer-generated image of a fractal construction of a tree.
On the right we see the phi or Fibonacci spiral branching off from a fixed iteration of the Mandelbrot attractor fractal set.
Just as the flat edged of the fractal and the volume of the quaternion slice represented two different forms of "holo" or "wholeness" replication, th fractal's jagged edge being the holograph and the depth of the strange attractor being the hologram, so, too, does the set of all regular patterns produced by feeding back transcendental numbers onto a fractal. The name for this third type of holography and holograms is "holognomic." Here is a depiction of how such a reguarly repeating pattern can be graphed from any fractional number sequence. Here, in this design of my own, we see the iteration of "infinitely repeating halves" is used. Such shapes as are generated by graphing transcendental numbers are called "gnomons."
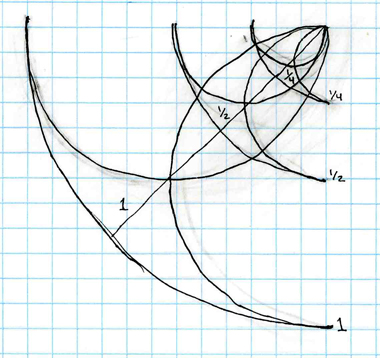
The "gnomonic" or harmonic "holo" -patterns can be thought of as the result of "auto-correlation" or of making one part of the "holo" refernetial to another, such that tab A fits slot B, etc. The finest example I've seen of applying one form of "holo" pattern to another, in order to form a more averaged ratio of difference between them, ie. a gnomon, is an effect known as the "buddhabrot." The Buddhabrot design takes the mandelbrot fractal set and converts it into a refraction (or 3-d appearing) holograph. By taking one form of holograph or self-referential pattern and applying it to another it elevates the combination of both to a higher level than their combined sum alone. The difference is the measure of the holognomon. Here is the holograph of the Mandelbrot fractal, known as the "Buddhabrot."
-original image source: http://www.superliminal.com/fractals/bbrot/bbrot_rgb_small.jpg -site context: http://www.superliminal.com/fractals/bbrot/bbrot.htm --------------------------------------------------------------- ---------------------------------------------------------------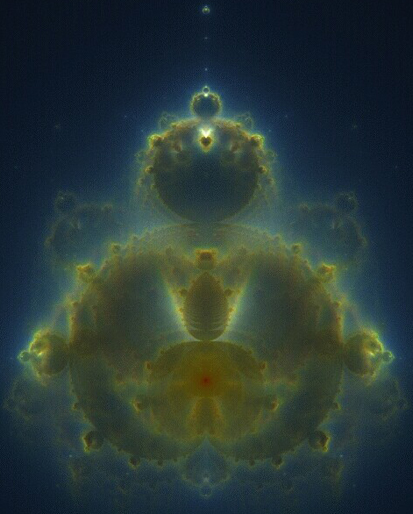
^click for high res^

