Here is how the "law" of three relates to the rule of fours, such as the four elements, or the three spatial directions over time.
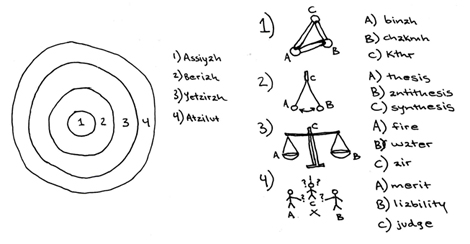
According to the Zohar, for example, there are four kabbalistic "worlds." According to the reckoning of the elders in the Zohar, there must therefore be a "law" of three in each of the four "worlds." And so they established judgment, balance, a pendulum and three supernals, three for each of the four, and thus, there were ten below three in one, and twelve altogether. This was pleasing to the elders because they saw that the "three in one" of the supernal tenth was the Right Knowledge of the Pythagorean Triangle, whose ratio of lengths between its three points is 3:4:5, and whose calculation is a^2+b^2=c^2.
This is a somewhat more scientific depiction of the essential topologies associated with the relative force-carrying particles for the four elemental forces of our local universe: http://www.benpadiah.com/MISC_diagrams/img534_copy.jpg More about this can be found on my site here: http://www.benpadiah.com/MISC_diagrams/pages/equations.html#RdS
This was all according to the reasoning of the elders, that is the Safeds of Spain, butit was based on observations made by their ancestors, that is, to us, the ancients. Just as we now study their Zohar, the Sefardic Septamanians studied the apocryphal scriptures of the Hermetic Pythagoreans. So, Moses DeLeon came to the conclusion that the "law of three" applied to the "four worlds" because the Pythagorean theorem could be applied to all of nature.
However, the four worlds themselves extend beyond only our local universe, which is simply the fourth comprised of nine subtended to the tenth comprised of three. This lowest, or material world, (Atzilut in the above diagram) was called Malkuth and was comprised of the four-elements as a shadow of the three dimensions of space and the fourth of linear time.
This was hinted at in the knowledge of the ancients, who tell us that the law of seven derives from the law of three applied to the four worlds no less than does the formation of the twelve. The four worlds of Hebrew Kabbalah and the seven worlds of Hellenic Greek Hermeticism were combined as the seven planets and the twelve houses of the zodiac even long before the time of the ancients, the predecessors of our own elders in keeping with this tradtion. This is because 3+4=7 just as does 3x4=12.
Therefore, we cannot necessarily say that the "law of three" does indeed apply to itself to form the nine to which we can subtend the tenth of three, and thus by which form the three plus one of the four. We cannot, therefore, even determine the difference between the five physical sense and the sixth sense of the psyche if we cannot distinguish the difference between the six psychic questions and the six physical directions.
So, what does this all have to do with "twinning"? Has it not been said that, in order to "self-deuplicate" we must go "three deep"? What, then is the third step of the process of self-duplication? It is simply realising for yourself, as if in an epiphany from a point of view above, that you are "twinned" with another, or with the idealogy of a group. To realise this, you must remember to "count yourself." When you "look through the eyes of another" you see through two pairs of lenses. Do not forget to count that which is doing the "looking" and "seeing" itself.
Now, the law of three, in itself, is quite simple. I have demonstrated how we cannot necessarily COMPOUND the law of three. That would be radioactive. That would be a pyramid scheme. No, we cannot multiply or double the "law" of three in itself. We cannot COMPOUND it, we cannot SQUARE it, we cannot DUPLICATE the law itself. The law of three is the law of three in itself alone. There is no law of four, no law of ten, no law of twelve, thirty-six, sixty-four or seventy-two for the law of three. There is only the law of the three for the law of three. From this third point of view, there is only that which is beneath and within itself. There is only the law of three in itself.
There is something interesting about the law of three: all the attributes so far discussed can be applied to triangles. The triangle itself is inherently six: three angles and three lengths. This holds true even on a curved surface, such as a sphere, where the angles can each be 90 degrees (forming 1/4 of the hemisphere). Here we see the 3 and the 4 of the ancients again, resembling the (3+2)x(4+2)=3x(3x4) of the five by six zodiacal dekans.
Here are the four basic fundamental types of triangles:
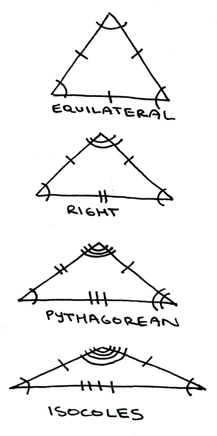
The equilateral trinagle's base angle is 60 degrees. The right triangle's non-right angles are both 45 degrees. The Pythagorean triangle's base angle is 30 degrees. The base angle of the isoceles triangle is twenty.
Here are some special cases of these types of triangles where certain angles and certain lengths combine to form certain theorems.
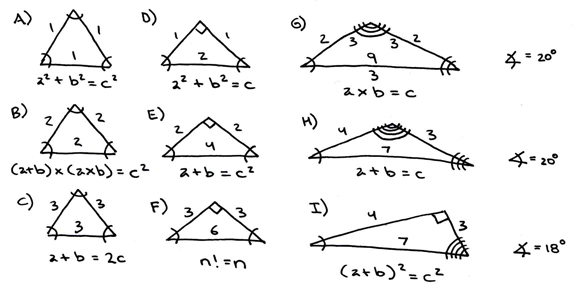
Now, let's consider the special cases whose equations are really restatements of one another, or rather, are the same.
Even though the ratios of lengths and angles are drastically different, we see equation H also applies to diagram E, that equation E also applies to diagram B, that equation I also applies to diagram H and vice versa, that the equation E holds true for the special case (3,3,9) of diagram G, etc. Let's consider a couple "special cases" in particular: diagrams A and F. We can see that equations A and F are interchangeable, and that the equation for A is actually the same as a^2+b^2=c^2, the Pythagorean theorem describing the base thirty Pythagorean triangle. Also notice the equations H and I are interchangeable between the diagrams H and I, and are a means of "factoring out" the squares of the Pythagorean theorem.
All of these being triangles, and all applying to the "law of three" all these different ratios represent different patterns of harmonic vibrational frequencies that occur not only within and through the realm of the mind (brain-waves) but also permeate and fill in the realm of matter. In other words, the "third step" of twinning involves mind over matter. The first step is telepathy. The second step mind-control. The third step is telekinesis. I'll come back to that in a moment.
Because all of these triangles have three angles and three lengths, any pair of three attributes can be assigned to any of these diagrams at once. For example: consider the special cases H and I. Now apply Kthr to the great angle, Chkmh to the mdeian angle, and Bnh to the least angle. Then define the seven subtended sefirot as length of the hypotenuse seven. Between Bnh and Kthr there are four (YHVH), but between Chkmh and Kthr there are only three (YHV). Again, three plus four is seven and three times four is twelve.
Let's consider two special cases more. Many of you are familiar with the saying "to square the circle" or "square circles." This saying dates back to antiquity, and the measurements of Pythagoras and his contemporary geometres. Although little of this material is available to us nowadays, more of it was available to the elders before its confiscation or destruction in the interim since then. Consider this "alchemical" depiction of the "philosopher's stone" as a geomtric depiction of the "squared circle."

The saying "to square the circle" actually dates back to the ancient reckoning of pi as a ratio between a circles circumference and its area. Pi, estimated by the ancients as approximately 22/7, is determined by comparing the radius of a circle and the square of the transcendental number, Pi. To determine the area of the circle relative to the area of the square, you have to "square the circle." This is done, basically, like the following:
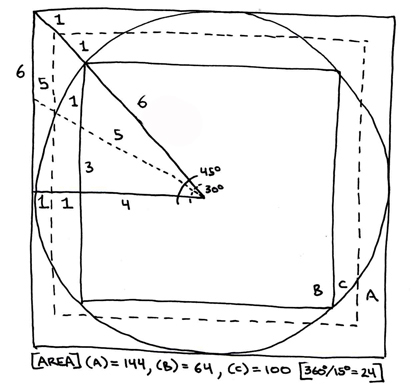
You can see many of the "special cases" of triangles involved in this diagram. This diagram basically depicts three areas: A) the greater square, B) the lesser square, C) the area is the same for both the middle square and the circle. Further examination of the difference in degrees yields the origin for the difference between the 360 degree circle and the 365.25 day year.
The primary components of the "squared circle" are the 3,4,5 Pythagorean triangle and the 45/45/90 degree right triangle. Although neither of these are "special" in this case, nonetheless we can see many, now familiar, triangles hidden within.
Of course, it is also common knowledge that if you graph the squares formed by these two types of triangle: the 3,4,5 Pythagorean and the 45/45/90 degree equilateral against one another, then you will form the phi/pi spiral. However more on this matter need not be said now.
So, after all this, what does it mean to "self-duplicate" or to "twin"? It means to go "three deep." This means that, through learning to see through another (telepathy), to speak through another (mind-control), and finally by applying (teleknises) the law of threes (triangles) to physical objects (vibrational ratios) we can learn mind over matter.
More about squaring the circle:
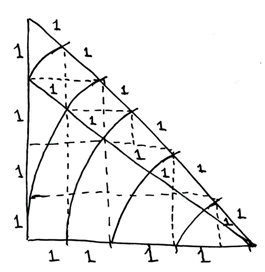
Here is the crux of the Pythagorean Triangle, conjoined at the measurement of the "Golden Mean" with a right equilateral triangle.
The non-right angle measures are 45/45 and 30/60, such that between the "upper" and "lower" triangles there is a measure of fifteen degrees difference.
In the above diagram all the units numbered "one" are the same measure.
There are two ways to apply the "Golden Mean" of the Pythagorean triangle to determining the area of a circle. One is to measure the radius of the circle as the base, longer, horizontal leg of the triangle. The other is to measure the radius of the circle as the hypotenuse of the Pythagorean triangle. Although these are both essentially the same model, you can see that, applying the former method (radius=base leg) to the basic theorem, you will be measuring a smaller amount of space than if you measure by applying the latter method (radius=hypotenuse).
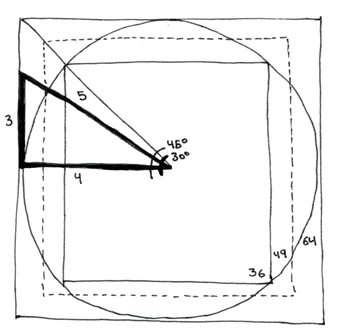
Therefore notice that the use of the "Golden Ratio" harmonic number sequence of 3:4:5 yields base 6,7,8 square circle areas.
The second type of "Golden Ratio" application of the Pythagorean triangle has already been shown (at the end of my last post, above). It is the same as the one I now give here (below) in that the radius is five in both.
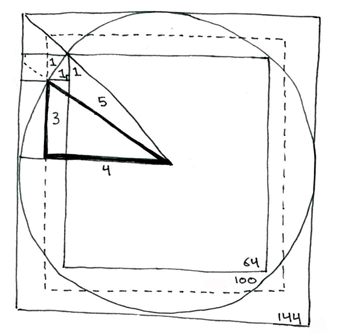
Here we can see that, by measuring the circle's radius as the hypotenuse of the "Golden Ratio" Pythagorean triangle, we can yield the larger areas of the base 8,10,12 squared circles.
Therefore, these are the two ways to yield a "square circle" from applying the Pythagorean triangle with its "Golden Ratio" of 3:4:5 to split the fifteen degree angle difference between 45/45 fractal expansion (base twelve hypotenuse) and the 30/60 gnomonic expansion (base ten hypotenuse).
These lengths for the hypotenuse/radius of the square/circle are derived by continuing to follow the gnomonic and fractal expansion rates up to base 12,13,16 areas.
Here are all the fundamental measures for the Pythagroean square/circle formula for any figure up to circle radius eight.
All of this is quite a bit more useful than you might at first think of it. Consider that, using this method, you can find the area of the earth. Consider the following chart, incorporating actual distances and degrees relative to our little blue jewel.
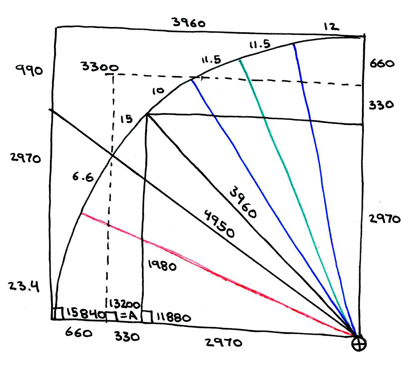
The red line indicates the tilt of earth's rotational axis from perpendicularity to the ecliptic plane of the rest of the objects in our solar system. The green line represents the precession of the gravitational, geographical pole. The blue lines represent the current variable offset, 11.5 degrees, between the geographic and the electromagnetic poles.
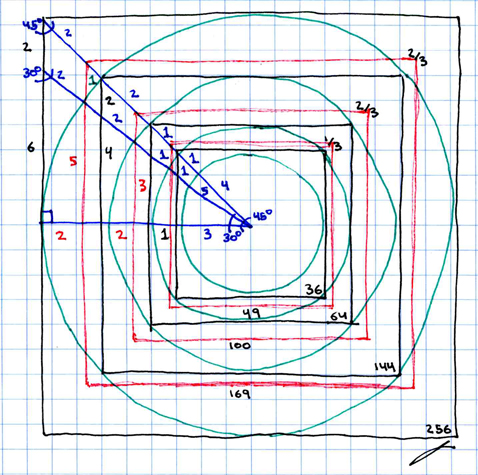
Here is a depiction of some of the smaller applicable scales of squared circle, particularly those from the two square (with area four) through the eight cube (area sixty-four). Note the special cases applied at certain points of intersection between the squared circles.

As you can see, by attaching an arc from each "special case" in point in the above diagram (depicting the very small square circle areas), one forms two spirals, one spiral arm whose angle of inclination (36 degrees) is determined by the angle of the Pythagorean triangle (let this spiral be called PHI), and one spiral arm whose angle of inclination (45 degrees) is determined by the other angle, of the "equiangular" triangle (let this second spiral be called PI).
Here is a diagram depicting the complete two spirals for up to area 256 (square circle sixteen):
(!don't stare too long, you'll go blind!)
---------------------------------------------------------------
---------------------------------------------------------------
