original MISC
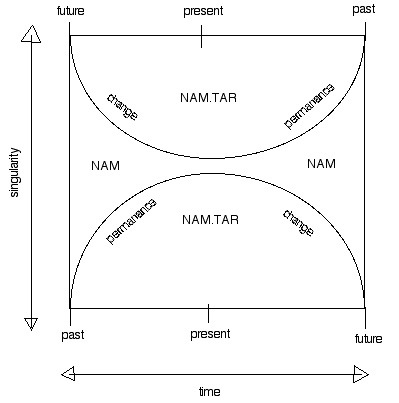
1A) this is the standard graph of above and below the limit of photic light which defines time as the standard arrow of entropy. Below, time progresses left to right, and above, opposite this. NAM (destiny) and NAM.TAR (fate or free will) increase and decrease in direct relationship to one another. The past is increasingly fixed (permanance) while the future is ever-more in flux (change). At either "end" of the timeline is a singularity connecting the above and below.
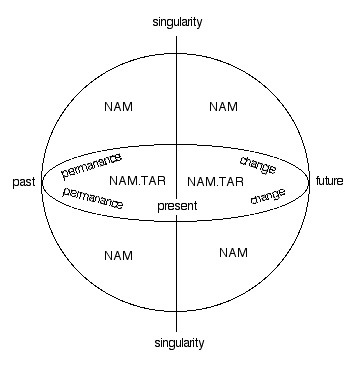
1B) when the standard graph is mapped onto a sphere, the relationships between above and below photic entropy become even clearer, as the apparent "twin" singularities are revealed as only a single polar axis, and the future and past below connect to their counterparts above around the equator, which is NAM between the two hemispheres of NAM.TAR. Change or permanence are then seen as the direction of rotation.
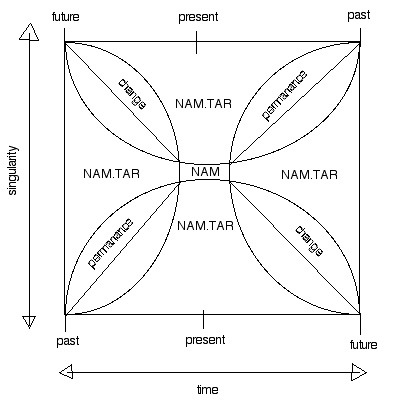
1C) In the second iteration of the standard diagram, the apparent "twin" singularities are both mapped as time-strems themselves, perpendicular to the standard time streams above and below the rate of photic entropy. The reason for doing this is to signify the multiverse and nulliverse effects of the aleph sub n toroid. Here we see that the same quanta are measured (photons on the left and below and tachyons above and to the right). Also we can more clearly the permanence and change become diaganol axes of effect by the interaction of these quanta.
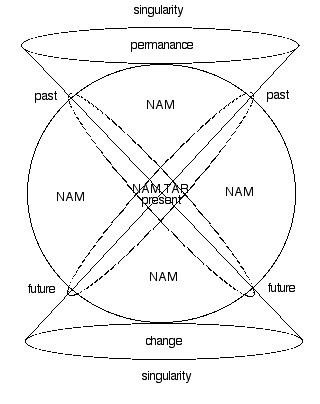
1D) When the second iteration is spherically mounted the reason for the double diaganol axes can be seen. The opposite corners of the transform map to each other and the double axis is revealed to be merely the precession, or rotational tilt, of the axis of the singularity. At ~ 45 degrees to each other, the equators (still NAM.TAR) of the apex of the rotational tilt of the polar axis are at ~ 90 degrees to one another, or perfect perpendicularity.
Discuss this section on the forums
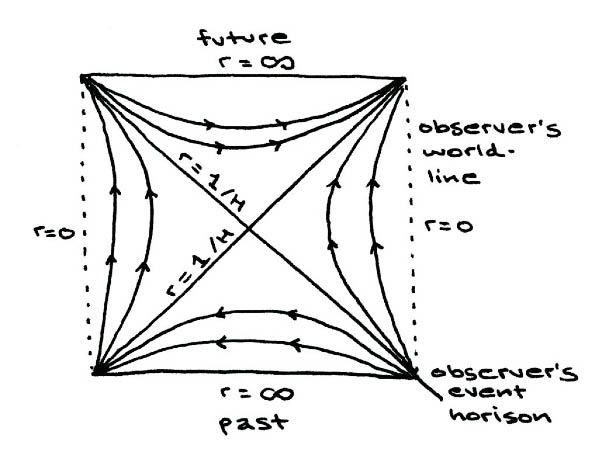
2A) This model represents the static DeSitter metric, which, as Hawking points out, describes a cosmology which is similar to a black hole. In DeSitter, it is empty and will expand exponentially at a fixed temperature. While Hawking points out the difference between this and the observed universe (which is relatively full and a non-fixed temperature) the DeSitter metric may yet describe the properties of underlying super-symmetric strings or branes which comprise the fabric of the space-time continuum's geometric surface.
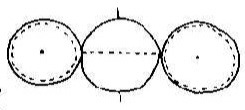
2B) What the DeSitter static metric describes is a unification by super-symmetry of the closed geometry of Euclidian space (the middle sphere, right) and the open geometry of Lorentzian-DeSitter space (the space between the outer spheres, right), where the radius = 0 on either side of the static metric is where the polar axis is a singularity. Since observers can be in varying places in the "space-like" past or future (infinity), their views represent diaganols which would be equivalent to the precession of the polar axis of the central sphere (right), when the singularity is replaced with a duration and becomes an event horizon.
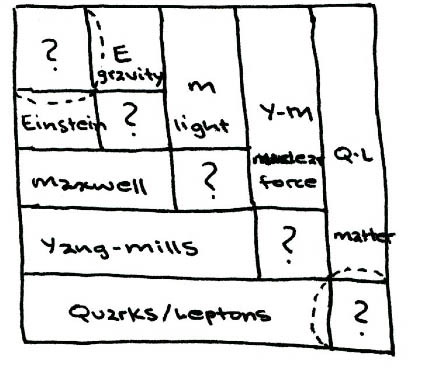
2C) The model to the left represents the super-Reimann metric tensor. Originally the Reimann metric tensor was a collection of 10 numbers, represented as 16 variables, describing the curvature of four-dimensional space. When extended to n-dimensions, the Reimann metric tensor also provides for sections of curvature that describe Einstein's equations for gravity and, through super-symmetry, those of Maxwell for photic radiation, Yang and Mills for the nuclear forces, and, theoretically, for matters particles such as quarks and leptons.
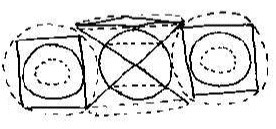
2D) The super-Reimann and DeSitter metrics are essentially in agreement, that is, they are complementary. The empty corner spaces in the super-Reimann are rightly filled by the static DeSitter. The reason for this is that the empty spaces in the super-Reimann at first appear to resemble a series of squares, that is, exponential expansion, however their scale relative to one another is arithmetic. Thus, we see they are all complementary to, and, actually, overlap one another. The three spheres (right) are only different positions of one sphere, whose polar axis precesses.
Discuss this section on the forums
3A) Here we see the combination of the DeSitter and super-Reimann metrics, with the elemntal forces duly marked, and with the second iteration of the standard graph acting as a short-hand for the elements within 4-d spacetime, and the DeSitter shown properly for sub-gravitic and super "cirtical mass" spatial curvatures, which are really complementary, and one and the same. The two, sub/super spacetime static metrics act as two parallel branes which attract toward one another, until the diaganol event horizon is warped into the ploar axis singularity of one or the other, forming a new universe through blackhole-like conditions.
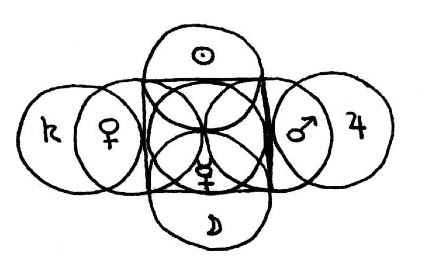
3B) The geometry of this mechanism (described by the formula: manifestation = the precession of dimension, or, by the shorthand phi/pi) has already ben thouroughly described elsewhere (see tau sub tau). Here, we see the diagram for this basic geometry seen at 45 degrees and at 4-d antipode. The seven spheres involved can be likened to the seven historically known planets, as well as to the seven color spectrum. In the center is the second iteration of the 4-space static DeSitter short-hand.
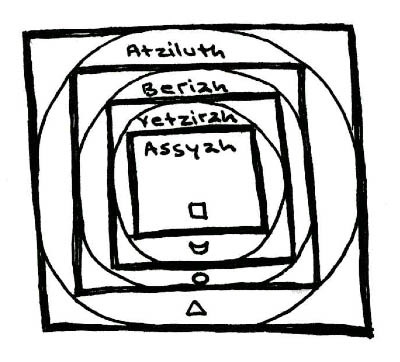
3C) When enlarged and rotated from 4-d antipode to apogee the second iteration of the static deSitter short-hand assumes a nested appearance. The spiralling involution / evolution which will become the universal light cone should be apparent by the light of chockmah. Here we see the equation expressed in the ancient names and the primordial satvas. Another expression for this is the serpent of kundalini wrapped around the Akashic egg.
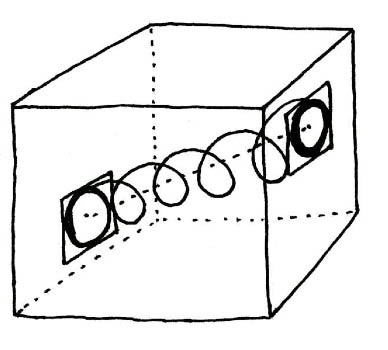
3D) If we take the 4-d apogee short-hand second iteration of the DeSitter metric and drop one dimension, we obtain a cube containing a diaganol. This differs from the standard diagram describing chaos theory only in that here we see the diaganol is a spiral, representing entropy over time which serves to further limit the chaos factor.
Discuss this section on the forums
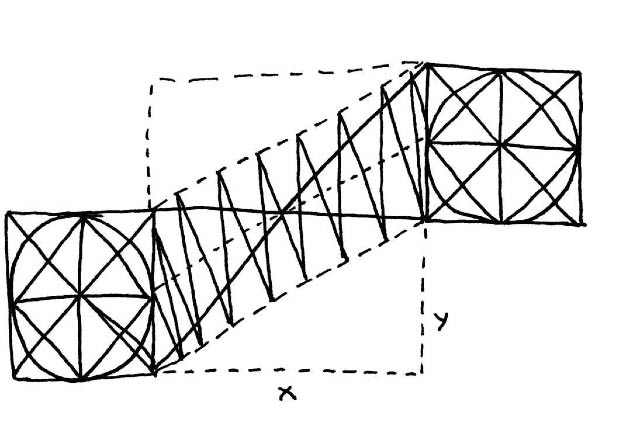
4A) Here we see the previous diagram from the side with the top and bottom of the spiral "unfolded." We see the difference between the standard chaos factor (the dotted diaganol) and the spiral in that the x & y variables of the spiral may repeat, while those of the standard chaos factor do not. To map these we use a dual/diaganol Cartesian quadrant.
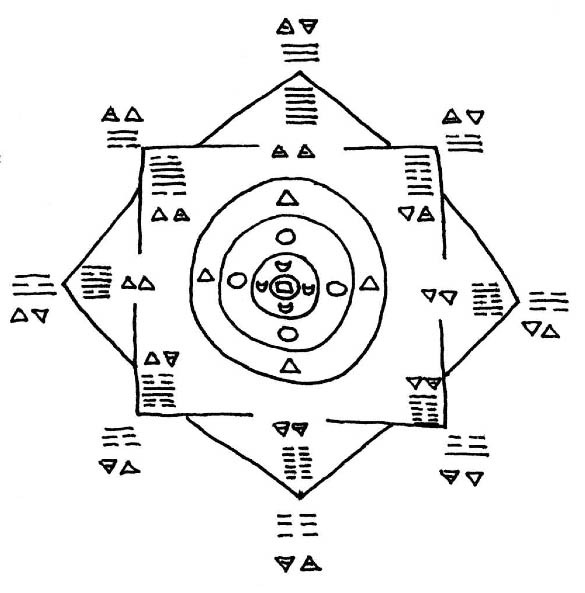
4B) The labelling of this quadrant, since it measures the spiral of entropy over time, is based on the four elemental forces of 4-spacetime. These are represented as the western alchemical, eastern trigram and satva symbols, and positioned around and within the quadrant geometry of the spiral, such that, as the world line orbits along it, the different combinations occur in a counter-rotational sequence.
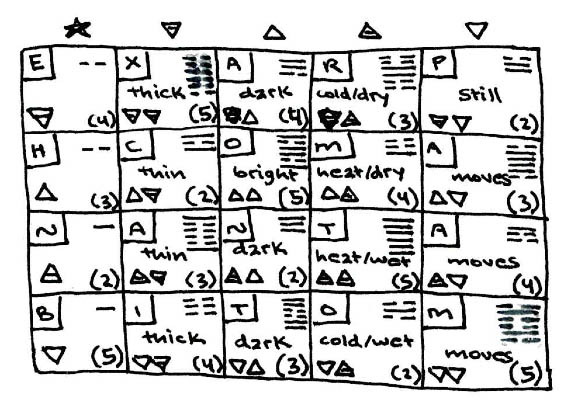
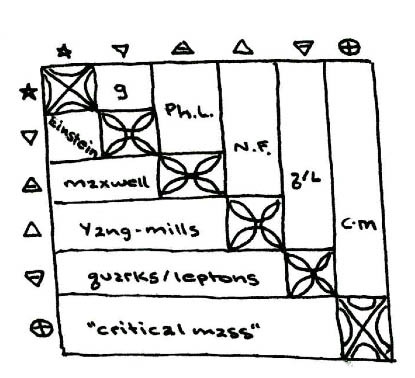
4C) The combinations of elemental forces can be plotted on a periodic chart. The numbers in each square's lower right corner represent the degree of difference from the square below, where the lowest of each column connects to the same column's top. The attribution of letters derives from the Enochian, and the other traits are self-explanatory.
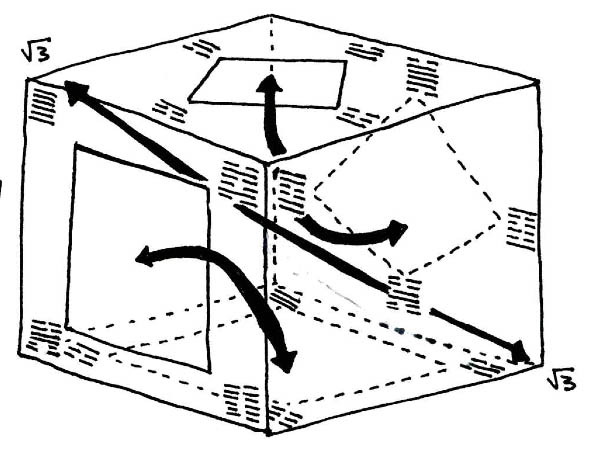
4D) When we return to the model of chaos theory we can further map the demi-elements onto the exterior (or as a median, interior) of the cube. Here we see, by the relationships between these attributes, that the elongation of the singularity into an event horizon by the extension of duration establishes the standard diaganol measure of chaos as a fixed diaganol sqr.rt. of 3 (from corner to corner). The relationship between the demi-elemental attributes and the corner-to-corner sqr.rt. of 3 chaos factor is that of a lorentz transform, to wit refer back to the first iteration of the standard graph (preceeding).
----------------------------------------------------------------------------------------------------------------