Tau Sub Tau
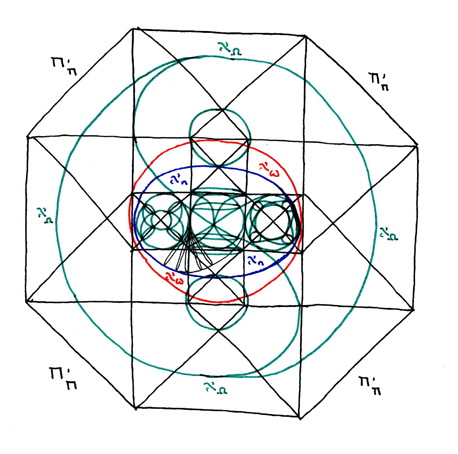
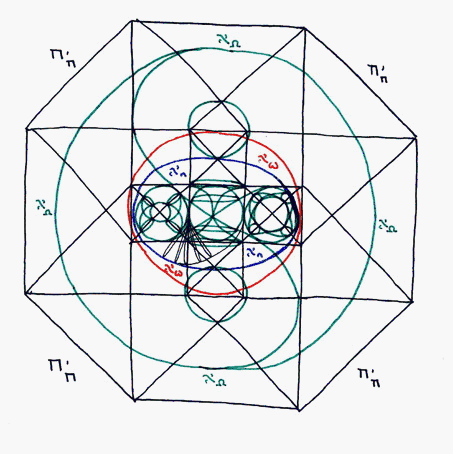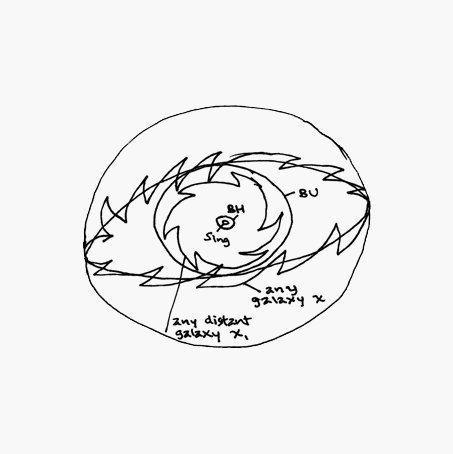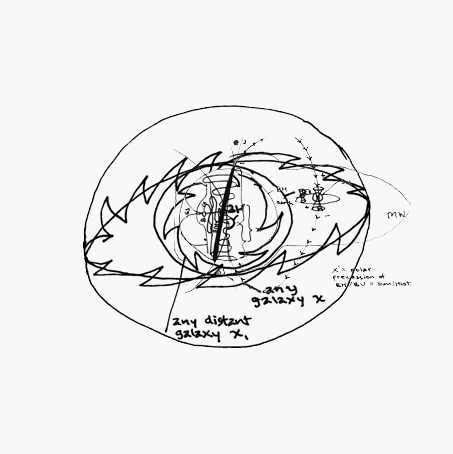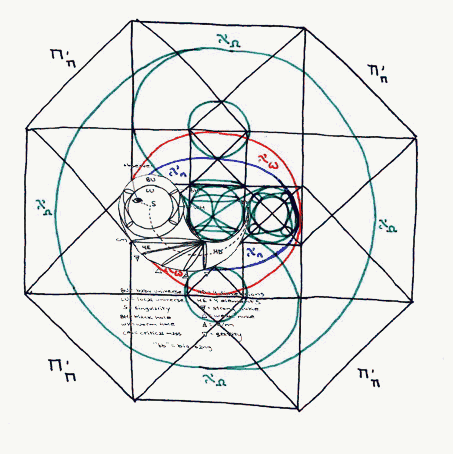
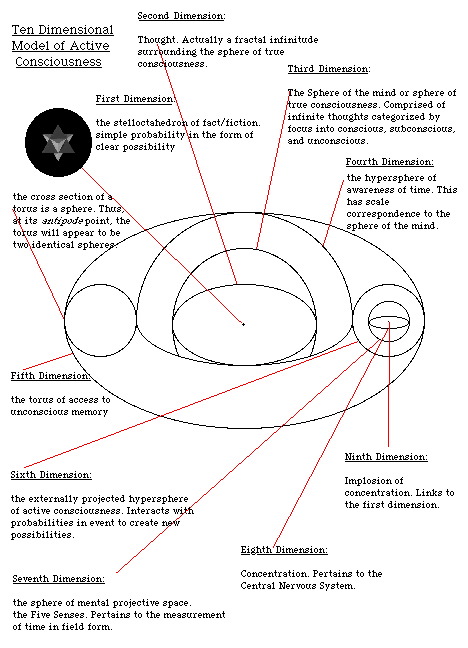
here we see the entirity of existence as it is known to me.
In the center is the blue toroid, at antipode (45 degrees). It is labeled aleph sub n.
Around this is the same toroid, represented in red, turned 90 degrees. It is labeled aleph sub sigma.
Around this is the greater hyperspehere of which the red toroid is the center. This greater hypersphere is represented in green. It is labeled aleph sub omega.
Encasing the entire structure is the tesseract geometry of the hypercube of time at antipode (45 degrees), labeled tau sub tau.
----------------------------------------------------------------------------------------------------------------here is the explanation for the titles.
There are variegated levels of infinity.
The lowest (irrationals) includes only transfinite numbers such as sqr.rt.2, sqr.rt.-1, pi, phi, etc, as well as variables such as e, c, h and h-bar. Irrational numbers represent singularities: expressable in compact variable form (sqr.rt.-1, sqr.rt.2, phi, pi, e, c, null, h, h-bar, etc.) such that, as axioms they can even be used in equations, they extend off infinitely. It can be proved that this set possesses 1:1 correspondence with the sets of natural numbers (non-zero positive integers) and counting numbers (positive integrers and zero), but common sense tells us not ever given number is irrational and that zero has quantifiable value as a place holder. Natural numbers are second dimensional: only positive integers not including zero, they have a binary beginning (1) and ending (infinity = null ~ zero). Counting numbers are three dimensional: they have binary beginning (0,1) and again, an ending that stretches off into the infinite.
Next come the integers (positive, negative and zero) then the rationals (which also include fractions). Integers and rational numbers are fourth dimensional. Wormholes occur as infinite fractionality breaks through between whole number integers. Since decimals are asymptotically infinite between any two whole, real numbers, the wormholes curve out to infinity and then bend back, like solar prominances, to open up between two other real coordinates. The infinite points of certain wormholes, as well as other infinities not connected by certain specific wormholes, are the Irrational numbers in between the whole, real integers, and these are the inversions of the rational number set that describes their entire potential area.
The reason the first three dimensions are spatial and the fourth dimension ephemeral is that Irrational, Natural and Counting Numbers are all denumerable by 1:1 correspondence. The Integers and Rational numbers though are an infinite list, related like a fractal to one another (where the empty spaces are the irrational black holes).
Beyond these numbers ‹ which are equivalent in set theory to different sets of sums, multiplicatives and powers using sigma as the symbol for the highest letter variable value past and given number (n) ‹ there are different transcendent infinities based entirely on variable letter symbols, such as infinity (sideways 8), 0bar (the "null" or empty set) and aleph (transinfinity) as well as n and sigma.
The first of these types of shells shows us that an inifnitely empty set is less than any given number, and therefore equal to zero as the origin point.
Beyond this is the aleph sub n set or transfinite set of n dimensions, and beyond this its multiplicative set. There is no additive, or sum, set, because aleph sub zero + n = aleph sub zero. This is because aleph sub n is a set and +n or -n represents a single coordinate vector, or local gauge displacement. The multiplicative set (2^aleph-sub-n... n^selph-sub-n) defines coordinate space in which for such a vector to allow movement of a local neighborhood.
Above and beyond this are the variable powers and their multiplicatives. Here we see the theory for set vector is given by the continuum hypothesis: 2aleph-sub-zero = aleph-sub-one; and by the generalised continuum hypothesis: 2^aleph-sub-alpha = aleph-sub-alpha+1 ... (n ^aleph-sub-sigma = aleph-sub-sigma+1/2n). This accounts for a neighborhood sheet upon which localised vector can be calculated.
Finally (to date), we have aleph-sub-sigma4 set, which translates in latman's terms to transinfinite continuum, with a transfinite dimensionality, that casts a shadow which is at least 4-dimensional, and at most (n) equal to inifnity. This is the lattice manifold on which the neighborhood sheet of coordinate vector set transformation occurs, yet it is still only representational of something beyond physical conception and altogether intangible.
--------------------------------In other words, we can use simple mathematical set theory to describe the boundaries of physical phenomenon. Where these numbers approach infinity, we can compare this to approaching the speed of photic radiation. Where these numbers transcend infinity, we can compare this to measurements beyond the limitations of our universe placed on it by this measure. Therefore, the subinfinite numbers (not pictured) represent the universe bound by photic radiation. The transinfinite numbers (pictured) represent that which is beyond our universe.
----------------------------------------------------------------------------------------------------------------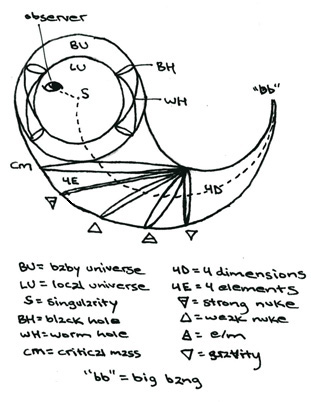
Now, the local universe is depicted in the small green circle to the left inside the blue torus. It is a circle inside another green circle. The inner green circle is our universe today. The outer green circle is the limit of the multiverse formed of all the baby universes inside the singularities inside back holes (represented here by the two hour-glass like shapes between the inner and outer small left circles).
Below this you will see five small elipses in thin black. These represent the developmental stages of each of the four elemental forces (from right to left: gravity, electromagnetic, weak nuclear and strong nuclear) and, to the furthest left, the point of "critical mass."
The somewhat larger green circle on the right side of the blue torus represents the nulliverse.
The local universe is fromed from and passes back into the hour-glass shape in the center circle as it alternates with the nulliverse.
These circles are depicted in more detail in the seven planets diagram (diagram 3B in ).
Discuss this section on the forums
------------------------------This is all the instruction on this diagram I can think to give at this time.
Figure 6
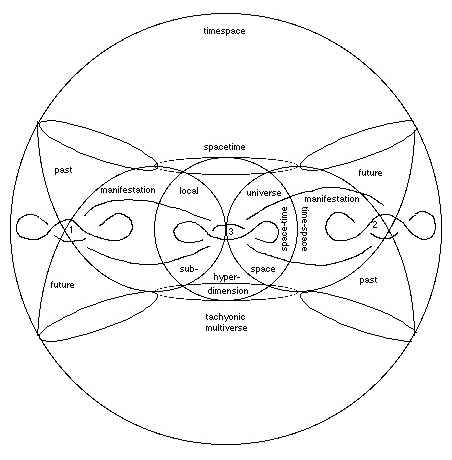
This figure shows an enlargement of the small left green circle inside the blue/red torus from the tau sub tau diagram.
It is clearly marked.
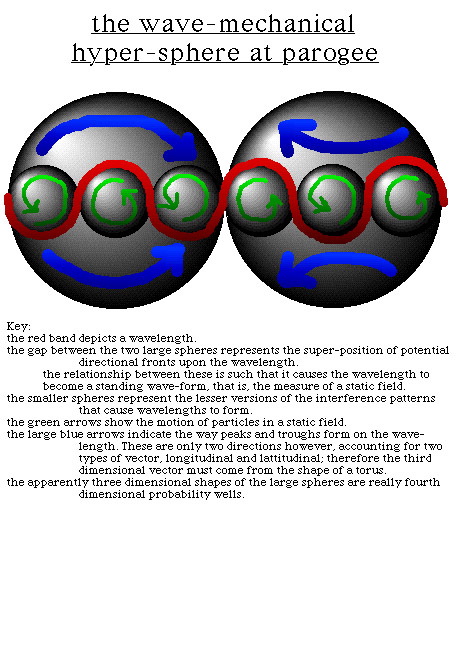
position 1 shows a toroidal manifold representing the sum over history of a black hole. It has a past (upper) and future (lower) light cone representing its history, which is comprised of wormholes (also represnted by the light cones).
position 2 shows this same toroidal manifold blackhole sum and lightcone wormhole history after a certain degree of fixed rotation.
Therefore there are two type of rotation of a black hole: A) that which is internal to the event horizon (the light cone wormhole histories) and B) that of the gravitational singularity itself. The rotation of the wormholes manifests itself as the rotation of the black hole around its gas jets. The rotation of the gravitational singularity manifests itself as the gradual precession of the axis of these gas jets. This is how they appear interior to our 3-spatial/4th-temporal dimension inside the spacetime continuum. Outside of the boundary of this continuum, determined by the speed of light squared (c^2), in 4-spatial/5th-temporal timespace, the same rotation of the event horizon and precession of the gas jets appears (as in figure 6) as a toroidal manifold (the precession of the grav. sing.) and the lightcone histories (rot. of ev. horiz.).
Postion 3 of the same shows another placement in the toroidal orbit of the toroidal manifold (the sum over histories). In this position, we can see how tachyons from the tachyonic multiverse feed in, through the past history ligthcone wormhole, through the toidal blackhole, and thus from hyperspace (labeled as hyperdimension in figure 6) into the subspace of the local universe. We see this from within 3-space/4th-time (or simply spacetime) as the gas jets of blackholes.
This entire toroidal orbit of the toroidal blackhole sum (the precession of the gas jets due to the rotation of the gravitational singularity) is labeled manifestation. This is because the matter/energy that leaves spacetime subspace through the wormhole event horizon surface of blackholes, flows out into the tachyonic multiverse, into the past history light cone. It then proceeds through the toroidal manifold sum of the blackhole's precession> It is then forced out through the future lightcone history wormhole to be blasted from the event horizon surface of the blackhole into subspacetime as the gas jets of the black hole.
This seems like a complicated process. However it will become easier to visualise (though perhaps more difficult to explain) with the next figure. For now all we need to know is that the precession of manifestation (the process of tachyon recycling) is = to the orbit of dimension (the tachyonic multiverse comprised of all toroidal sum/histories of black holes) and that the precession of dimension (the toroidal manifold sum over histories of the entire multiverse itself) is also = to the orbit of manifestation (the combined rotations of any given black hole). In plain english, what we see as a singular process OUTSIDE in timespace (the multiverse) is also seen as multiple physical events INSIDE in spacetime (the universe). And, in the simplest terms possible, the inside of the universe is also equal to the outside of the universe.
Discuss this section on the forums
Figure 5
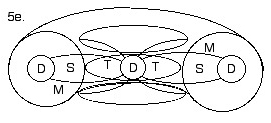
since I am working backward from the tau sub tau diagram, we will start with figure 5e. and work backwards to 5a.
5e) this figure shows the cross section (at antipode or at 45 degrees) of figure 6.
the abbreviated labels represent as follows:
D = dimension (the tachyons which are being recycled through the blackholes)
M = the orbit of manifestation (the precession of that dimension)
S = space, the 3-spatial component of spacetime
T = time, the 4th dimensional component of spacetime
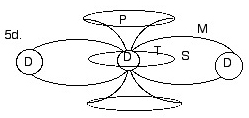
5d) this figure shows a simplified version of the same cross section.
the abbreviated labels remain the same; one more has been added.
P = precession
the difference here is that the lightcones histories of the wormholes (the circles around the dimensional positions) and the toroidal orbit of the tachyonic multiverse they comprise are not depicted.
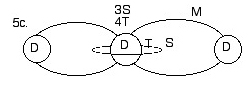
5c) this figure shows a further simplified version of the cross section.
Here we can see that spacetime (3-space/4th-time) is only comprised of the dimension (depicted as position 3 in figure 6) which is in the center position. We also see that space and time form an orbit around this centre dimension, in the same way the histories of the wormholes formed one around the outer two positions of dimension. The interior of this orbit is Time, while the exterior is space.
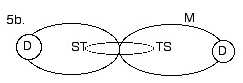
5b) this figure shows the same simplification as figure 5c, however without the central dimension depicted.
Here we can see that there really does not need to be a dimension occupying this central position for the rest of the model to work. Also, we see that, since time is interior to the orbital plane around this central position, then spacetime can occupy a position on one side of it, while timespace occupies a position opposite.
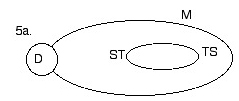
5a) this figure shows a further simplification of figure 5b, however with the orbit of manifestation unfolded from its depiction as a figure 8.
Here we can see the simplest version of all the preceding figures. Pure Dimension (tachyons) orbits in an elipse (manifests) around a small orbit which comprises the space-time-space continuum. In plain language: the alternation between space-like and time-like characteristics of dimensionality is known as, and depends on degree of, manifestation.
Discuss this section on the forums
Figure 4
this figure, which might seem complex, is really quite simple in the context I have presented this material.
It is, for all intents and purposes, identical to a basic version of figure 6.
However, while figure 6 represents the multiverse containing the universe...
this figure represents how consciousness itself can be depicted by the same model.
Since each part is self-explanatory, I will not belabour the point by explaning it further.
All I will say is that, while prior models of consciousness (such as the iceberg model, etc.) do not do so, this model can account for parapsychological processes such as ESP between sentient lifeforms and PK telekinisis.
Discuss this section on the forums
Figure 3
this figure represents the process (by arrows) through which the same type effects occur through the two models depicted in figures 4 and 6.
Each large circle is broken up into a torus, and all the parts of the torus are seen to counter-rotate.
There is a more detailed explanation of the individual component processes involved at the bottom of the page.
Discuss this section on the forums
Figure 2
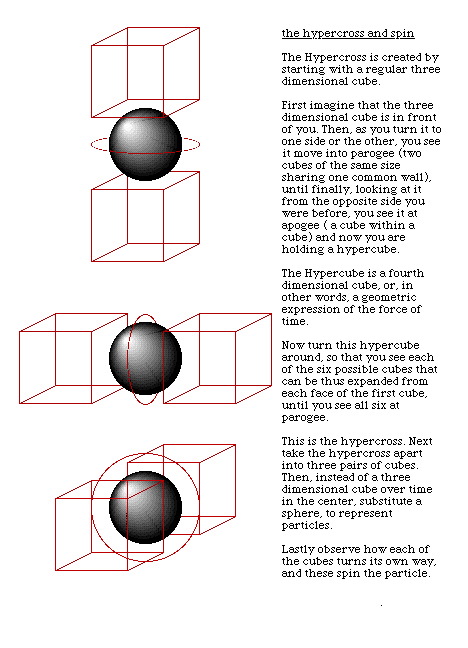
this figure shows how the processes depicted as circles (and toroids) in all the previous figures can also be represented by cubes. For each direction of rotation of the sphere, two cubes oriented in a congruent direction can be used also to express the same rotation.
Discuss this section on the forums
Figure 1
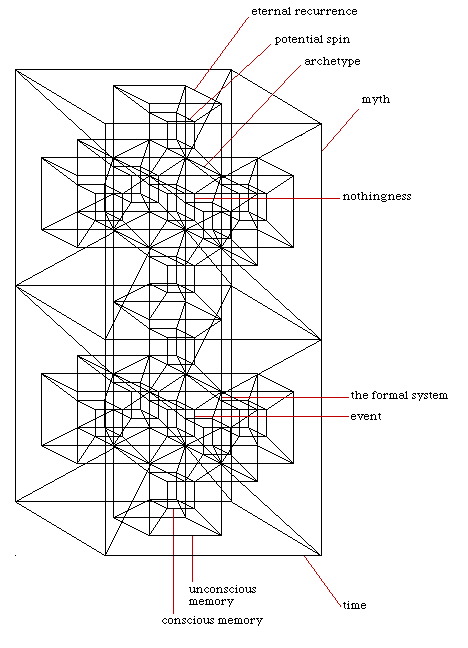
this model may appear complex at first also.
However, it is simply the expression using cubes (as explaned in figure 2) of the combination of figure 6 (above) and figure 4 (below).
Each part is labeled, so I will not belabour the point by over explanation.... But I will say this...
the hypercubic hypercross contained within the above hypercube represents the contents of figure 6 (the multiverse) as it would be perceived by figure 4 (consciousness).
Discuss this section on the forums
FSOM complete
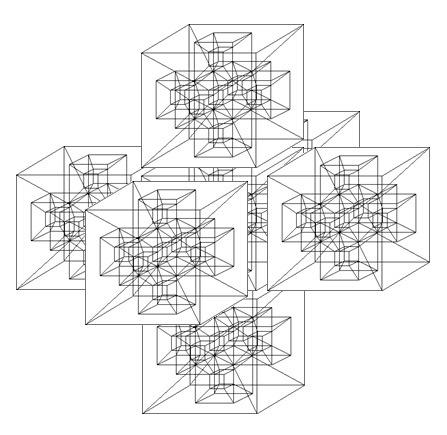
this figure corresponds, more or less accurately, to the structure from which the preceeding model may be withdrawn.
It should be noted here also that the external (superior) cube in the preceeding model would be the same for any given axis of outer (inferior) cube. This would also hold true were the superior and inferior cubes in the above model reversed relative the axes of rotation of the exterior cubes in this figure.
FSOM base unit

An eight-cornered stelloctahedron can be extrpolated from the eight-cornered cube. Here we see that certain traits may be assigned to these eight corners. These traits, one each assigned to each corner, are the six fundamental questions of reasoning, Had (determining necessity or certainty) and Not (determining uncertainty or impossibility).
The eight-node stelloctahedron is the same as two, conjoined tetrahedrons. Just as, from a point of view above the midpoint of one of the tetrahedron's edges, the shadow of the tetrahedron would assume the outline of a square, so, too, is the shadow of a cube, when seen from above one of its corners, a hexagon. Likewise, the shadow cast by the stelloctahedron, when seen from above one of its corners, a hexagram.
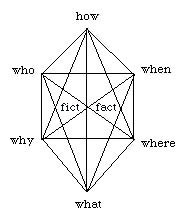
Here we see the hexagon shadow of a cube, with its nested hexagram shadow of the stelloctohedron. The same six fundamental questions of reasoning are arranged around the external nodes, with two more ‹ fact and fiction ‹ as the two points (front and back) at the centerpoint of intersection.
The arrangement of the six fundamental questions of reason around the inversion point of fact/fiction is based on the relationships formed between each node and every other node by the short legs of the hexagon, the medium legs of the hexagram, and the long legs of the three dimensional radial axis.
For only a brief example, the three vertical legs connecting (from left to right) who-why, how-what, and when-where, conjugate as the three pillars of philosophical legislation, that is, the spiritual, ethical, and physical.
------------------------------------------------------------------------------