-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
the hypercube
A point is one dimensional. A line (the side of a plane) is two dimensional. A cube is three dimensional. A "hypercube" is four dimensional.
The shadow of a line (seen from above one end) is a one-dimensional point. The shadow of a cube (seen from above one side) is a two-dimensional plane. So, too, the shadow of a hypercube is three dimensional.
If one were to turn it around in three dimensions, a cube can cast two-dimensional shadows of different shapes. For example, the shadow of a cube seen from above the midpoint of one of its faces is a square. The shadow of a cube seen from above one of its corners is a hexagon. Etc.
So, too, as one rotates and reorients a hypercube in four dimensions, it casts three dimensional shadows of different shapes. It is by the shapes of these shadows alone that we can rightly describe the movements of the hypercube.
Just as there are certain angles from which a cube can be viewed that cast regular shaped shadows ‹ the hexagon, the square, etc. ‹ so also are there certain angles and positions at which the hypercube will cast regular shaped three dimensional shadows.
One of these is, of course, the cube itself. The angle at which the hypercube casts a cubic shadow I call "standard position."
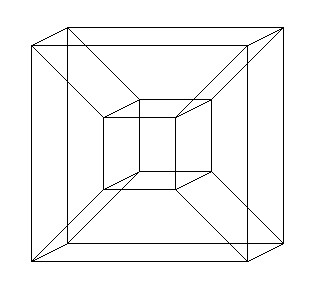
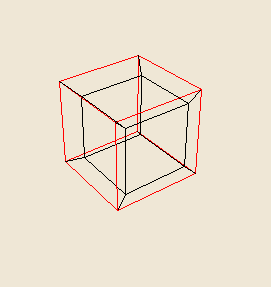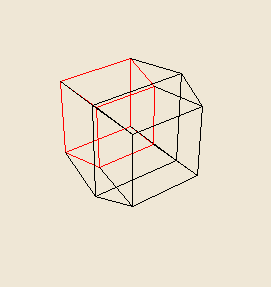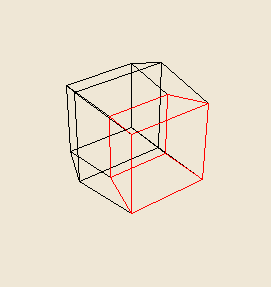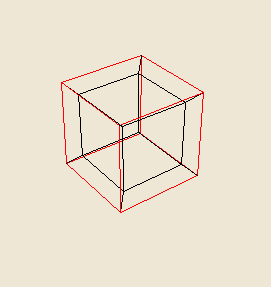
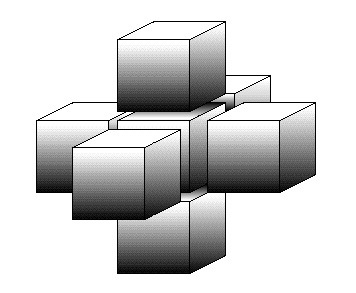
A hypercube also casts a regular solid shape at "nested position," and the shape it casts then is a cube-within-a-cube. This is shape is the one most commonly associated with the hypercube.
Here is a picture of the hypercube at "nested position" :
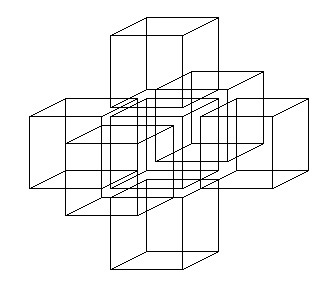
Another position at which the hypercube casts a regular shadow is what I call the "conjoined position." The shadow it casts at this position is a shape geometres know as a "tesseract." The word tesseract is another name for the hypercube.
Here is a picture of the "conjoined" hypercube's shadow, the tesseract:
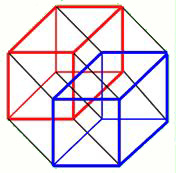
The last position at which the hypercube casts a regular shaped shadow which we will be dealing with here is called "antipode" position. Like the cube-within-a-cube and the tesseract, the hypercube at antipode also consists of two cubes.
The "nested" cube-within-a-cube shows one cube within the other, a view as above one of the faces of the hypercube. The "conjoined" tesseract shows one cube off-set from the other (by diaganols) and this is the view from above one of the hypercube's corners. The "antipode" position is a view from above one of the hypercube's edges.
Here is a picture of the "antipode" position of the hypercube:
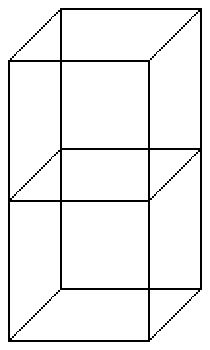
Remember, all of these regular solid shapes are only different shadows cast by the same hypercube. The only difference is that the hypercube is being seen from different angles.
Just as a cube casts different shaped two dimensional shadows as it is rotated in three dimensional space, so, too, does the hypercube cast different shaped three dimensional shadows as it rotates in four-space. The rotation of a hypercube differs from the rotation of a cube, however. Because a hypercube is comprised of two cubes, each with the same volume, its rotation moves one of these cubes through the other.
Here is a picture showing a few stages of this process:
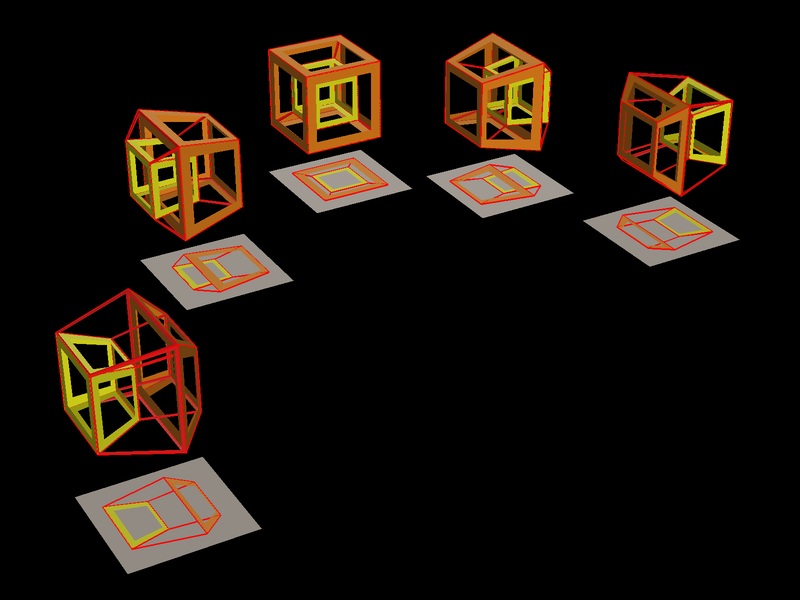
It should be remembered, however, that, just as the cube can be rotated around three axes of 3-space, so does the hypercube rotate through itself along a 4-d axis. This means that, while the simple rotation depicted above is occuring between two cubes on opposite sides, the same rotation is actually occuring for the hypercube through 6 cubes, 3 opposite 3.
Here is a computer rendering of the rotation of the hypercube:
Here is a depiction of a "slice" of a hypercube taken from one corner to the opposite corner:

Notice that the corner of the hypercube is a tetrahedron, that 1/4 through the hypercube is an octahedron, and that 3/4 through the hypercube is a zonehedral.
Discuss this section on the forums
applications of the hypercube
There are applications of the hypercube in many fields of study. Consider the following lattice which explains a complex series of relationships in quantum mechanics:
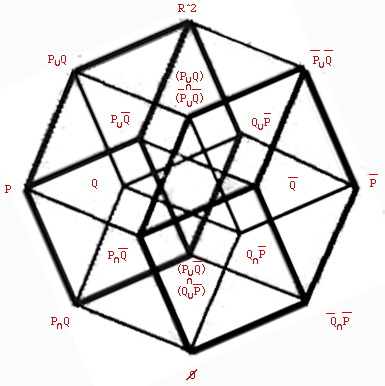
Also, ancient Hebrew mystics, when looking for an alternative to the tetractys of Pythagoras, stumbled upon the hypercube at antipode position for their "tree of life" diagram. Here, we see that each corner, or node, of the tree describes an attribute of YHVH, and that the twenty-two "paths" connecting these "sefirot" emanations are assigned to the twenty-two letters of the Hebrew alef-bet. This arrangement is called the Gra.
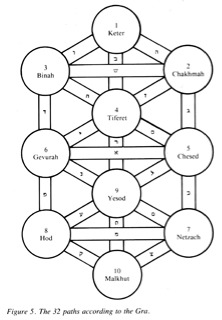
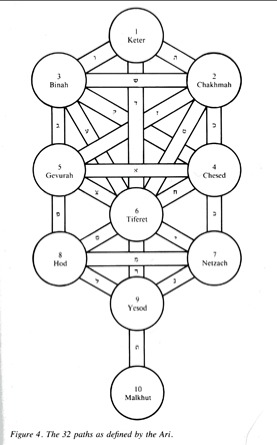
The tree of life diagram may be better recognised by its later depiction, rendered by the Safed school of Ha QBLH, known as the Ari arrangement.
-------------------------------------------------------------------------------
the hypercross
When an ordinary 3-cube is unfolded, it forms a cross of six unit squares:
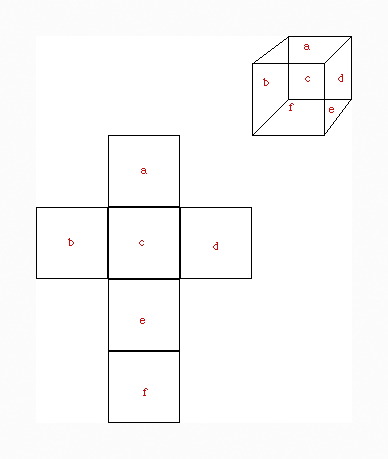
So it has been reckoned that when the hypercube is unfolded, it forms a cross of eight unit cubes. Here, we see that the central cube is surrounded by six cubes, one for each side, plus a subtended eighth cube.
Here is a depiction of this type of hypercross by Salvador Dalí:

However, this type of hypercross is comprised of eight unit cubes, while the flat cross formed by the unfolded 3-cube is only comprised of six unit squares.
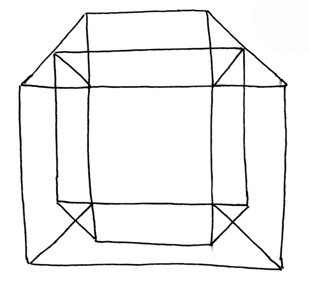
Another tye of hypercross can be formed without the subtended eighth cube. Like the unfolded 3-cube, it has six cube sides around each side. Here is a picture of it:
This type of hypercross should not be misunderstood as lacking the eighth subtended cube, however. The eighth cube is simply hidden within this form of the hypercross, between the six surrounding cubes and the central seventh. It is what is known as an "impossible" cube.
Here is a picture of the "impossible" cube in the hypercross:
This type of impossible cube was discovered, along with a similar impossible triangle, in the 20th century by mathematician Roger Penrose. Such impossible shapes were then incorporated into the architectures depicted by Dutch artist Maurit Cornelius Escher:

This type of cube is called "impossible" because it cannot exist in three space, although it can be depicted two dimensionally. Here is a wooden scultpure of the impossible cube. It is comprised of two separate sculptures, one above and one below, and then photographed at an angle which allows them to appear as if they were a single cohesive whole.

Discuss this section on the forums
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
PHI/PI
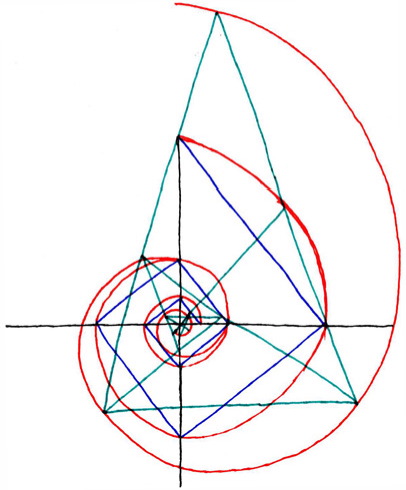
This diagram depicts a large part of what I work with on a daily basis.
It shows the orientation between what I consider, for shorthand notation, a pi and a phi spiral.
It should be noted that arithmetic expansion occurs unilinearly, as a diaganol vector on a cartesian coordinate graph.
Now, exponential expansion occurs when the exponent of the integer is increased. For example, if one takes the exponential expansion of the numberline of arithmetic expansion, such that, 1^2, 2^2, 3^2, etc... where it then forms the summed numberline, such that, 1, 4, 9, etc....
A third kind of expansion rate exists, however it has been considered more or less esoteric, because it forms a very specific inherent pattern when graphed. This kind of expansion rate is associated with the Fibonnaci sequence of numbers, such that, 1, 1, 2, 3, 5, 8, 13, etc... where the rate of expansion is determined by the addition of only the preceding two numbers to form the sum digit third in the sequence. When this sequence is graphed as points around an origin in a cartesian grid, it forms a spiral, and this spiral has been found everywhere throughout nature, from the branching patterns on plants to the proportions of the human body. This is the pattern I call, for shorthand, phi.
Returning to exponential expansion, we find that, when graphed around the origin point in a cartesian graph, this type of expansion also forms a spiral pattern. The difference between this, exponential, and the Fibonnaci spiral is that the exponential spiral is rectalinear, whereas the phi spiral progresses triangularly. This type of spiral, which is rectalinear and exponential, is what I call, for notation, pi.
The difference between them is the solution to an equation I refer to as phi/pi.
Above the origin point, phi appears as the upper central spiral, and pi as the lower central spiral.
Discuss this section on the forums
-------------------------------------------------------------------------------
Now, I would like to take a moment to compare some self-evident facts that we can observe in nature. I am not going to claim to have invented any of these things, as I hear doing so results in bad karma.
It is a self-evident fact, for example, that the seven basic colours of the spectrum of light (red, orange, yellow, green, blue, indigo, violet in order) can be mapped onto the surface of a torus, or hypersphere, in only one way, such that each of the seven colours occupies the same area on the surface of the shape.
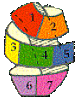
Now, once these colours have been mapped onto the surface of the torus, we see that the outline between each of the mapped areas forms a spiral that wraps around the surface of the hypersphere.

The spiral that outlines the seven coulour spectrum is, and this also is a completely self-evident fact and was not "invented" by any human hands, is a "phi" spiral.

Now, this "phi" spiral revolves AROUND the circumference of the torus (clockwise or counterclockwise) depending upon the rotation THROUGH the centre of the torus (outward from centre or inward toward centre, respectively) of the seven coloured areas mapped onto its surface.

In other words, the "phi" spiral revolves around the circmference as a MEASUREMENT of the surface of the torus. It MEASURES the fourth-dimensionality of this shape by MOVING, that is, it changes over time, and is therefore, like the clock, a means of measuring the passage of the fourth dimension.
However, this MEASUREMENT is only of the SURFACE of the torus, measuring the revolution from the circumference (seen from above) to the centre. This is a measurement of AREA, that is, of the combined seven areas of the mapped colour spectrum.
However, what if we measure the VOLUME of the torus, that is, the interior of the rotating radii of the hyersphere? Just as the "phi" spiral REVOLVES as it measures the SURFACE AREA, so too do we need a measurement device for the ROTATION of the INTERIOR VOLUME.
We know that, as the "phi" spiral "revolves" around the "top" and "bottom" of the hypersphere, so too, when we look at the torus from the "side" we see there is "rotation" of each radius, "right" or "left." Thus, just as the "revolution" of the "phi" spiral tells us about the external surface area, so too can the rotation of these radii tell us about the internal volume.
Now, when the "phi" spiral is revolving "clockwise" it means the torus is rotating "outward." When the "phi" spiral is revolving "counterclockwise" it means the torus is rotating "inward." But, just as the "top" rotates "inward" while the "bottom" rotates "otward," yet there are not two phi spirals, only one continuous spiral measuring the external area, so, even though there are two radii "sides" that rotate "clockwise" or "counterclockwise" respectively, there are not two different spirals, one for each radius, one moving "clockwise" while the other moves "counterclockwise," but only one cntinuous spiral measuring the internal volume.
So, we have "phi" measuring the outside, and another, single and continuous, spiral measuring the inside. I call this spiral "pi" for short hand, but the spiral I mean when I refer to this spiral as "pi" is really the "spiral mirabilis" derived from "e," the so-called "natural number." I have found that by dividing "phi" (1.1618) by "pi" (3.14) and adding one, you arrive at 1.37, which is the same as the so-called "natural" number. Therefore "e" would equal the combined "phi" (exterior) and "pi" (interior) spirals. This would mean that, if "phi" was both clockwise and counterclockwise, and "pi" was both counterclockwise and clockwise, as in the torus, then the "natural" spiral would be equal to the combination of their motions, that is, would be the sum of their spin, expressable mathematically as e=phi/pi.
All of these observations arise from self-evident facts of nature. None of them is my own personal invention, nor, I would posit, the "invention" of anyone other than the Creator of this universe, God. Therefore, please feel at utter liberty to discuss these ideas with no worry that I will oppose your applications of them. We are free here, and we are equal.
My own personal applications of this model, the "phi/pi" spiral model for the measurement of the fourth dimension and the hypershapes that exist therein, form the basis for my cosmological diagrams that I included with my published book, "the Metaphysician's Desk Reference."
discuss this section on the forums
-------------------------------------------------------------------------------

-------------------------------------------------------------------------------
