
Phi over Pi can be easily demonstrated using simple mathematics.
Apply the Pythagorean theorem, thus: (for any right triangle with legs A and B and hypotenuse C) a^2+b^2=c^2.
This can be depicted with a triangle surrounded by three squares. The base (number per side) of each square will be a sequential progression, such as 1,2,3.
Thus, for example, the square of 3 plus the square of 4 equals the square of 5.
Next, depict this as an ascending pattern of number squares and triangles, such that the greater leg and the lesser leg will swap places in the sequence and each order hypotenuse will become the greater leg for the next higher order triangle.
Here is a series of unit squares arranged in this manner from base 3 to base 9.
netsquares_1.jpg netsquares_2.jpg
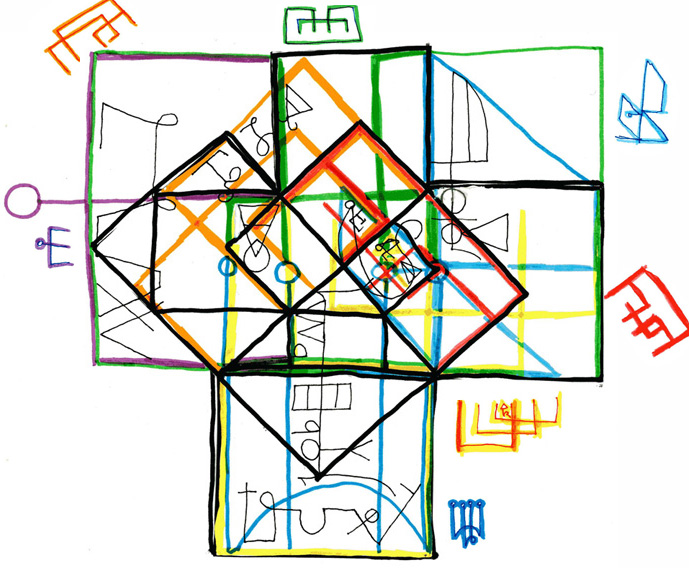
Now, if you arrange these triangles at right angles to one another (such that the same size leg squares overlap) they will form the pattern of the equiangular spiral.
Here is a depiction of this progression as a spiral using the above number squares.
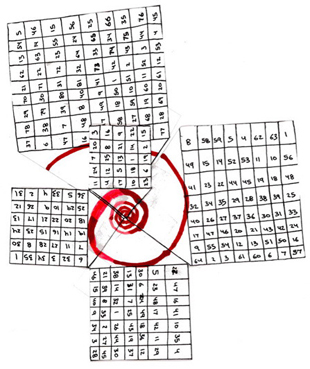
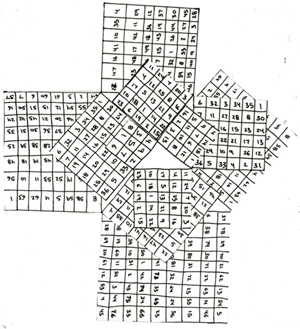
Two types of spiral can actually be extrapolated from this pattern. The equiangular spiral has been depicted. Now the Fibonacci sequence spiral may be extrapolated. It roughly connects the squares whose bases occur in its regular numerical sequence (i.e. 1,1,2,3,5,8,13,etc.).
Here is a rough depiction of the conjined pi and phi spirals on the pattern of the Pythagroean squares.
Now, this arrangement containing these two spirals can also be folded, and doing so renders a clearer representation in three-dimensions of the orientation of the one spiral to the other.

The pattern formed by the squares and triangles themselves also fits into the form of a tesseract (or a fourth-dimensional cube, or hypercube).
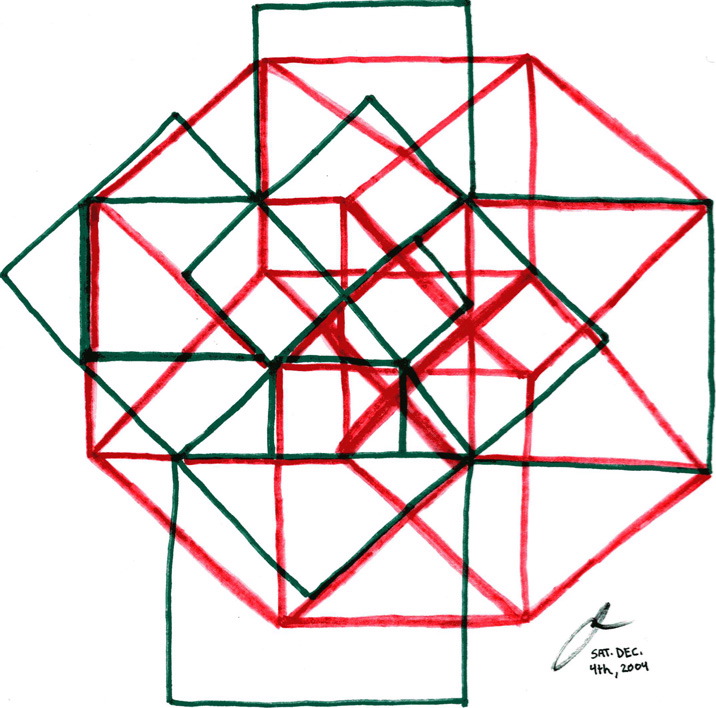
Discuss this section on the forums
an explanation of the method can be found here: chart one.
-------------------------------------------------------------------------------this information is all © 2004 Jonathan Barlow Gee
LINKS:
