chart 1
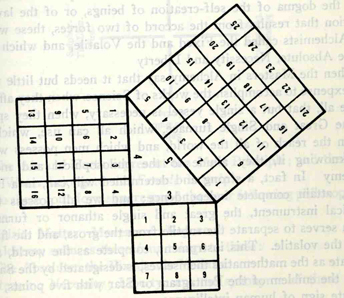
Let's begin by looking again at the Pythagorean theorem, and in particular the Pythagorean theorem triangle coined as Euclid's 47th proposition, the right triangle of legs length 3 and 4 and hypotneuse length 5. This particular copy of the Pythagorean, or Pi, triangle known as Euclid's 47th has been passed on along to us by the goodly Mason Albert Pike, and comes to us from page 789 of Morals and Dogma, his masterful work upon the subject of Free Masonry.
Considering exponential expansion of the base unit (such that the base-1 unit of a 9-square would be equal in area to the size of the three square, the base unit of which would be one-third of one-third of one nine-square base-1 unit, ie. 3^2=9 and ˆ9=3), we form the following sequence of Pythagorean triangles:
as further adumbrated upon here.
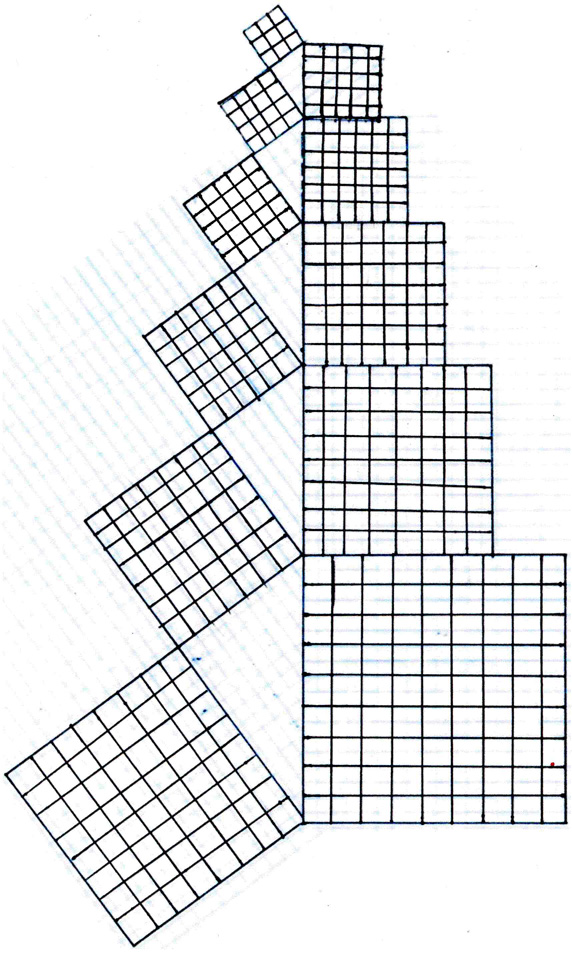
In order to distinguish which squares have the same area sized base units, we can label them using certain arrangements of natural numbers that can be determined from applying a simple formula based on the number of base-units in the area of the square. When we apply this formula, we see that there are really only seven different squares depicted in the above arrangement, since 4 of the 11 squares depicted are actually comprised of the same sized base unit, ie have the same area, as 4 of the other 7. The formula we will use to distinguish one square from another, then, is the formula that renders the above sequence as seven "magic number" squares. It is given thus:
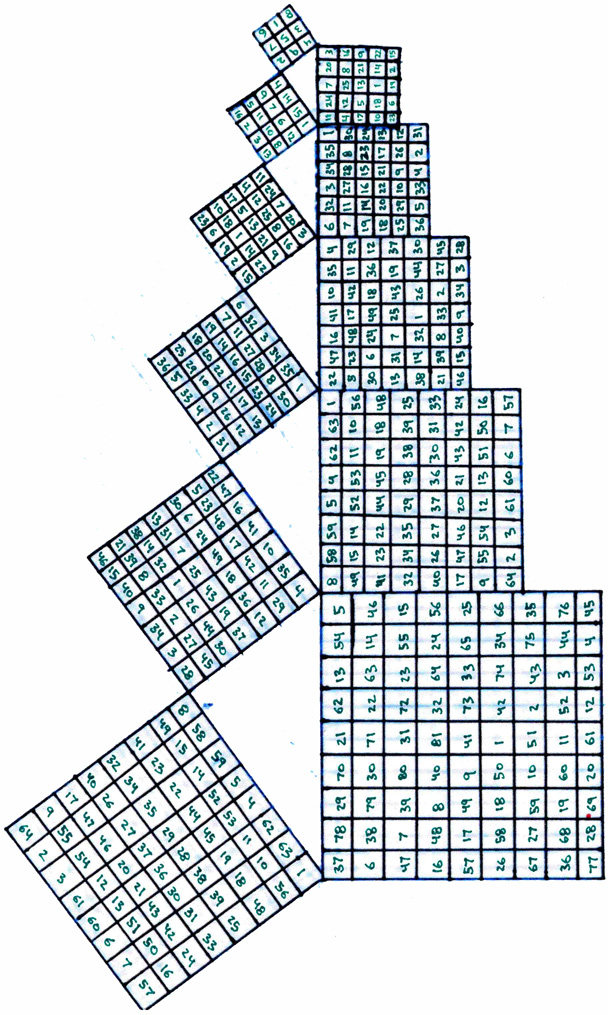
S = N(N^2 + 1)/(2), or rather N^2(N^2+1)/2, or even (N^4 + N^2)/2, or most importantly: [m(m+1)/2]/N, where arithmetically 1+2+3+...+m, where m = N^2 for N^2 base units per square, and where S= the "magic sum" of the N horizontal rows and N vertical columns of base units, as well as the sums of the main diaganols. Here are examples of the first, or smallest, seven number squares used to differentiate the seven different sized squares:
But don't forget that these squares are going to be different sizes from not only one another, but also from the sizes they would be if each had the same size base unit. Such an array as that would graphically depict arithmetic expansion, while the arrangement we are using here represents the first degree or type of exponential expansion. The Pythagorean triangle forms a Pi spiral, and this is the lower form of exponential expansion when compared to the Fibonnaci sequence of isoceles triangles that forms, in turn, an expontential Phi spiral.
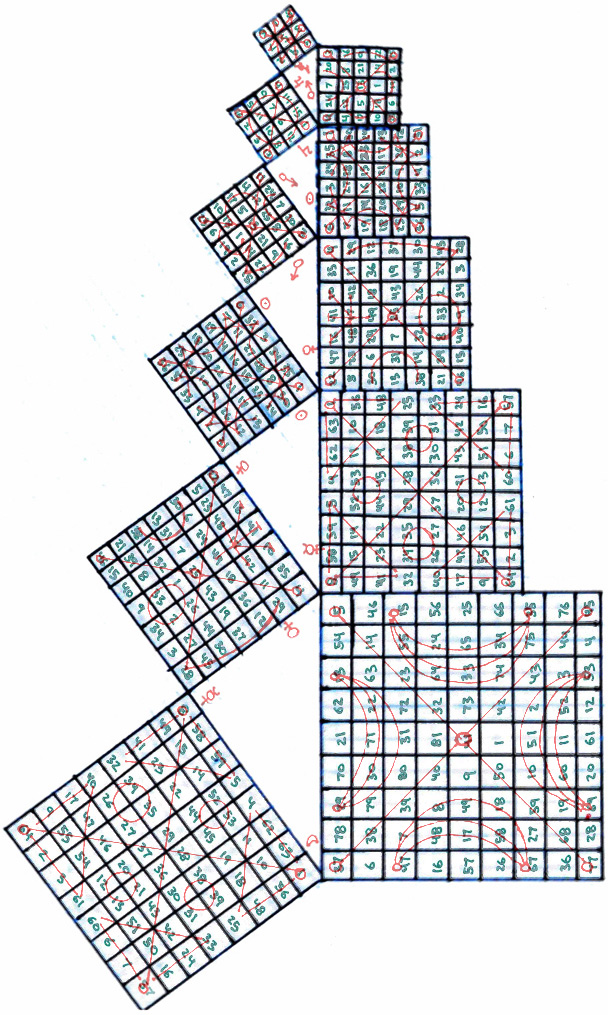
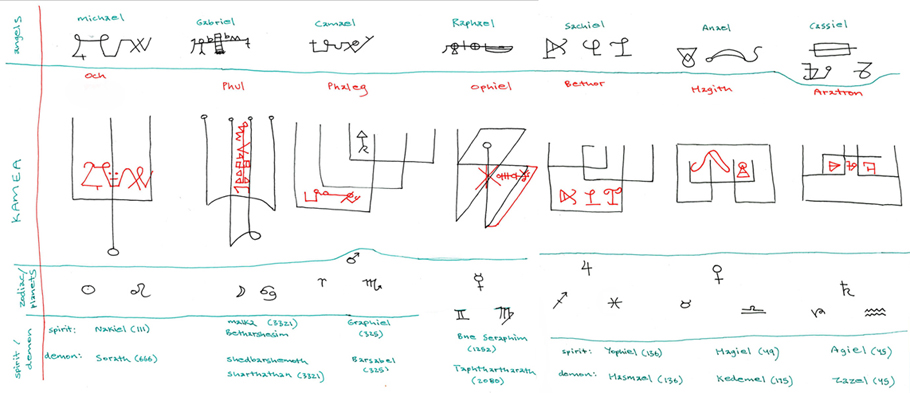
The "magic numbers" that are generated as sums on the matrix grid are by no means arbitrary. You should immediately notice that, the larger the base unit, and thus the larger the area of the square, the larger the "magic sum" becomes. This is not coincidental. It is a result of certain underlying geometric patterns inherent in different sized "magic number" squares. This geometric pattern is revealed by the sequences of numbers and how they can be moved about and transformed on the board without changing the "magic number sum." The practise of this revelation was called Kamea by the ancient Greeks, who worked as extensively with such "mathemagical" absurdities as "magic number" squares as they did more lucratively with trigonometry. They discovered the rotations and movements underlying the sequential relationships expressed as number matrices. The process of performing a transformation on a square of arbitrary area by rendering it a "magic number" square is called performing "Kamea" on the square, and thus the geometric depictions of these underlying currents below the numbers is called a "Kamea." Here are the Kamea for the first seven smallest "magic number" squares:
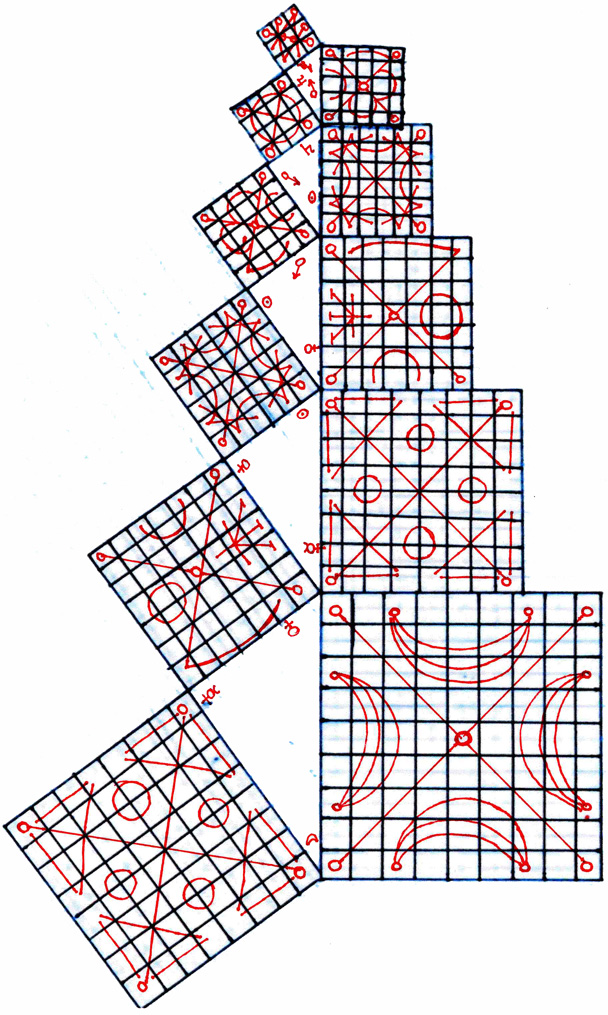
So, if we want to compare the Kamea, or geometric patterns underlying the number matrices, and the "magic numbers" forming the mathematical characteristics of these different ratios of sizes of square areas, we can depict the two of them overlapping as such:
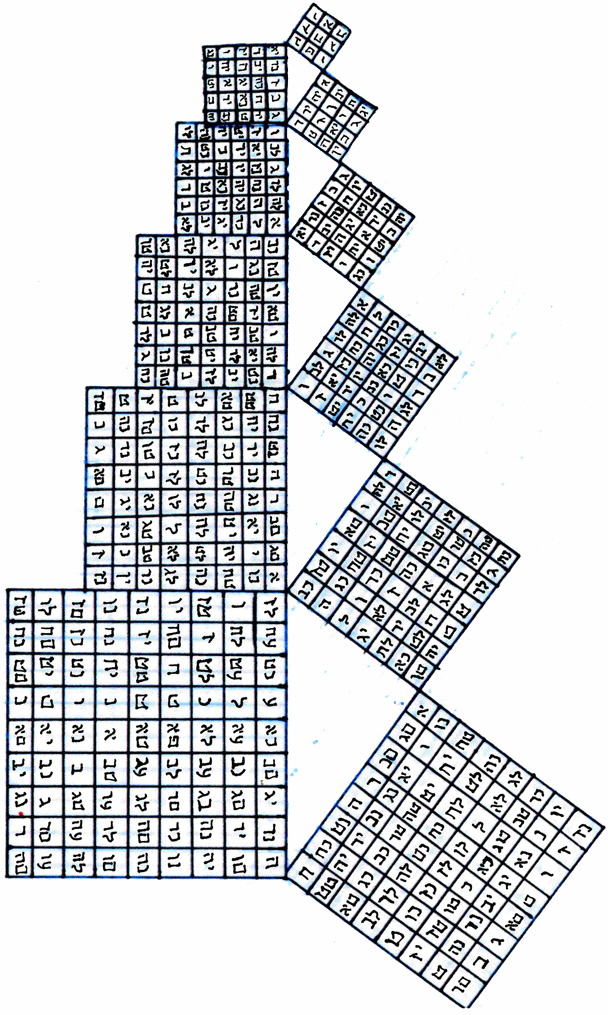
As an aside, the knowledge of these basic "magic number" squares is very ancient. As an instrument to augment meditation, that is, an amulet, they are preserved in their original Hebrew letters, where each letter or combination of letters was equivalent to a sum of the integer numbers each Hebrew letter represented. This process was called "gematria" and it was also a part of the tradition of QBLH, as well as was making amulets based on these specific "magic number" squares. Here is a brief excerpt on this practise as it relates to these specific number squares from the turn of the twnetieth century Egyptologist E.A. Wallis Budge:


Here are the Hebrew letters given for each square in the sequence of number squares. They are meant to printed on the opposite side of the combined squares, however if taken alone, they will form a three-dimensional spiral by rotating clockwise, as opposed to the preceding model which, if folded and taped to construct a three-dimensional spiral, will fold-up with a clockwise twist.
Because the ancients were aware of the "Kamea" geometric patterns behind the transformations of components of the "magic sum" number squares, and because they associated these with their folk superstitions of keeping amulets and talismans, they permuted and varied different Kamea patterns as many times as the numbers themselves could be transformed in order to form new ways to cast glamour spells and ward off toxic hexes. The result of this was a new form of Kamea, not based on the numerical geometries underlying the "magic sum" number matrices, but on some other, otherwise unknown measure of geomeric pattern. These were the earliest sigils.
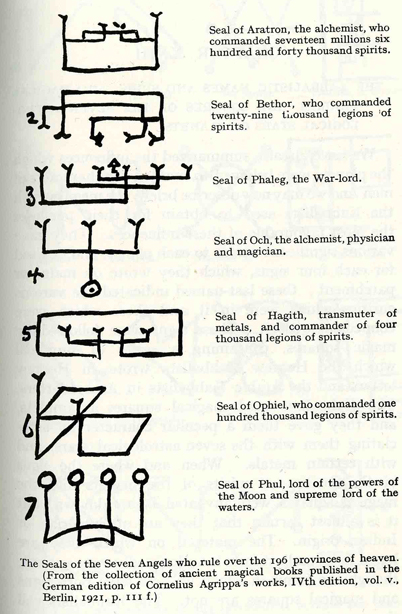
Budge traces these linear sigils at least as far back as Henry Cornelius Agrippa in the fifteenth century. They are also contained in the seventeenth aphorism of the third septenary of the 1575 manuscript the Arbatel of Magick (252 KB .pdf file), which traces their origin back to Zoroaster of Persia.
The seven number squares are now grouped as according to the seven planets of antiquity, each of which is attributed a metal in the western Alchemical tradition, and a chakra in ancient Buddhist yoga. Here is how each of the linear sigils is associated with each of the Kamea:
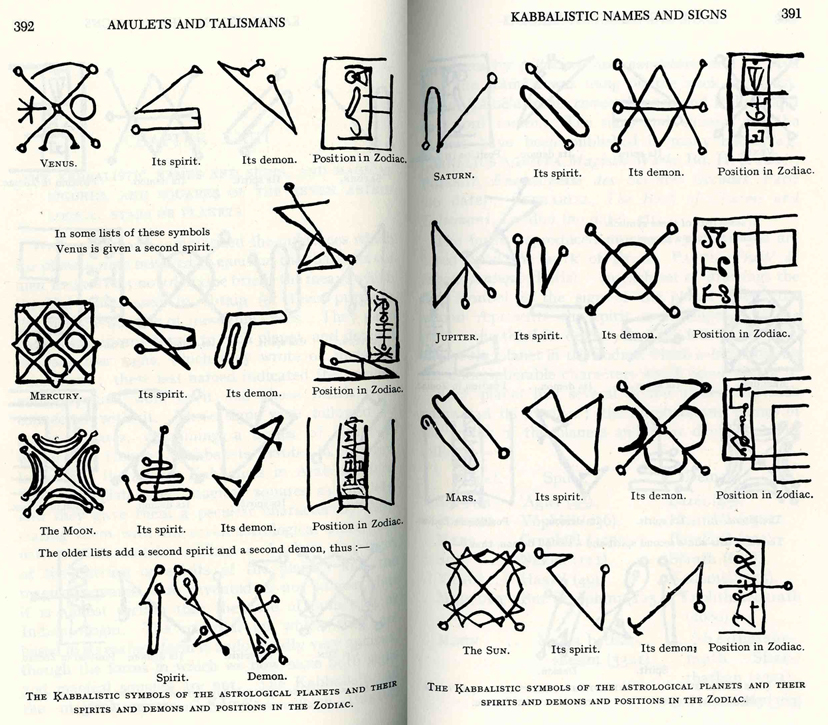
Introduced in this arrangement are another addition to the linear sigils, a second set of sigils, contained within the first, and being comprised of not only straight lines, as the "psitions in the zodiac" enclosing them, but of both lines and curves.
Here, these curved, linear sigils are given in the seventeenth century work "the Magus," which the introduction to the Arbatel reminds us is a Persian word in origin. Barrett further associates the seven "planetary" linear/curved sigils to the seven days of the week, a realm of Heaven, the name of an archangel, and either one or two signs of the zodiac.
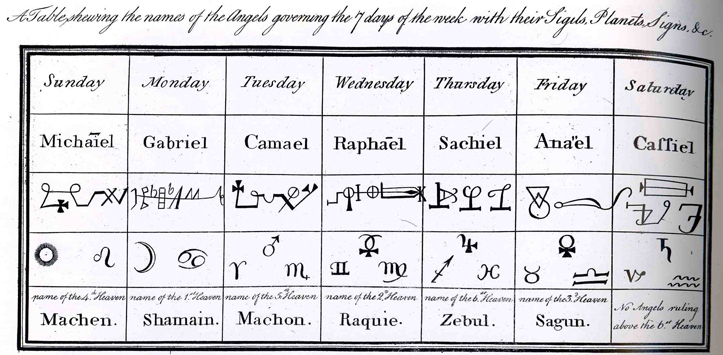
This is a comparison of the information we have compiled thus far: the upper row are the archangels, beneath that the linear and linear/curved sigils symbolising the number squares' kamea, beneath these the seven planets in twelve "positions," and beneath that the name of the spirit and demon beneath the archangels who are, in turn, over the legions of spirits and demons.
Now, if we take the seven archangels and we position them according to Barrett's twelve "positions" in the zodiac, the result appears as follows:
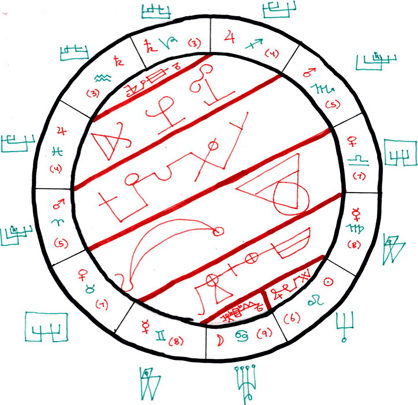
where the names, or sigils, of the seven planetary archangels are shown in red, and the kamea "positions" in the zodiac are shown in green.
If we take the topology of this shape and give it two "twists" while viwing it edge-on from the side, the result appears like this:
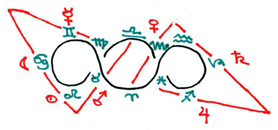
which, as it turns out, is one of the only arrangements of this configuration possible (out of a total of twelve, based on the varying positions of the zodiac) that will display this type of triangular symmetry when the same constellations are connected in the 2-twist transform of topology and the initial arrangement as proposed by Barrett. The three others are complementary to this position, displaying the same cardinal signs, only rotated into a different position along the double-twisted ecliptic.
Barrett's arrangement of the seven Archangels relative to the primum mobile of the zodiac determines them as a fixed alignment. Unlike the moveable or changing (cadent) triangular alignment formed in the 2-twist topology, the fixed or Archetypal topology proposed by Barrett does not fluctuate through a series of regular polygons. Instead it retains its shape regardless of which other way it is turned.
At this point it should be noted that the last two diagrams show the same shape, only from different angles, and that the seven lines forming the bars across the zodiac in the first image (101), and the seven forming the triangular alignments in the 2-twisted topology (img022), are actually depicting the same alignments along the flat plane represented by the green ecliptic of the zodiac.
So, with that caveat, let us compare this circular or 2-twisted ecliptic zodiac and its accompanying seven Archangelic or Archetypical alignments. It should also be remembered that all of what we are talking about now are only geometric expressions for the combinations of 3 and 4 in the forms of addition (3+4=7) and multiplication (3X4=12). The primacy of the multiplication process to the addition process is equivalent to the supremacy of exponential expansion to arithmetic expansion and the rule of the Fibonnaci spiral over the Pythagorean spiral, or phi/pi.
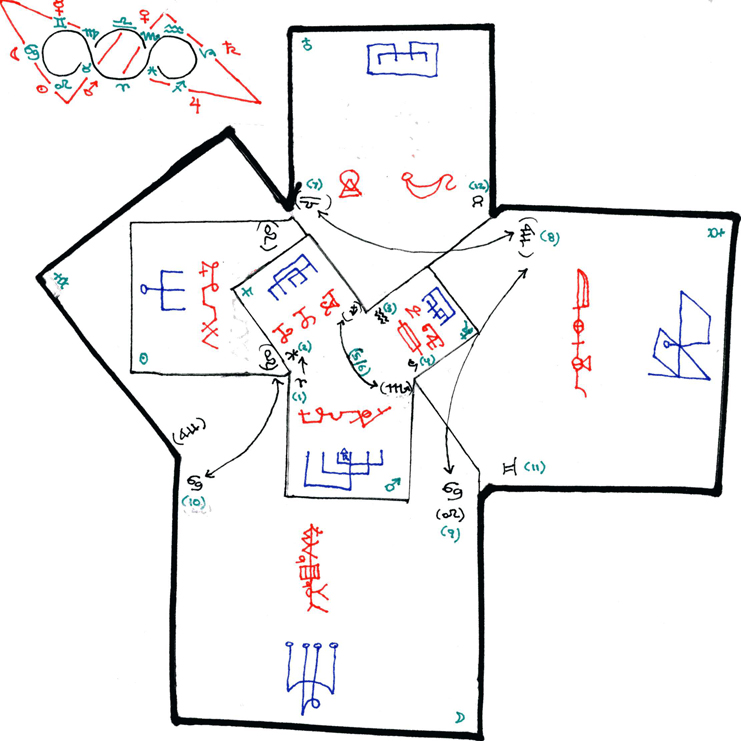
Here we see the same arrangement as in the last two diagrams, only here the topology of the ecliptic zodiac has been transformed onto the surface of the Pythagorean expansion rate spiral formed by folding up the Kamea squares. Instead of being written across between 12, the 7 are dominant in this model, while the 12 are merely expressed as components of the model's folding pattern. That is, rather than the twelve surrounding the seven, in this model the seven surround the twelve.
Now we will examine the origin of the linear-only sigils, the so-called "positions" in the zodiac of Budge, to compare them to the more familiar model of the ecliptic zodiac used in astrology and navigation.
(To construct the Pythagorean triangle, or Pi exponential, spiral from the various area sized squares given here, please refer again to my section on the Pythagorean Spiral.)
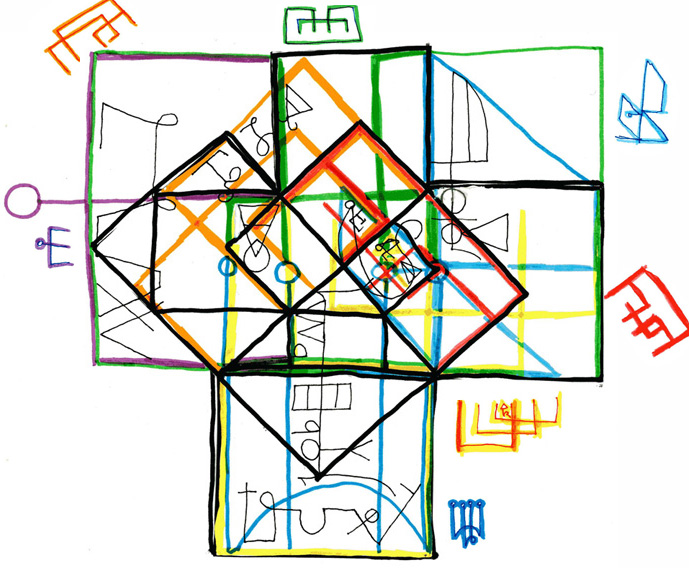
Above is the immediately preceding diagram with the same labels, only now they have been expanded so that, instead of being written on the area of the square, they enclose and encompass the entire outline from above and beyond it. Here they are labeled according to the seven colours, but their placement in the model is derived from the angle of the correspondent planetary Archangel to the "position" in the zodiac. To confirm this, each Archangel's linear/curved sigil is placed within and upon the composite form comprised of the component "positions."
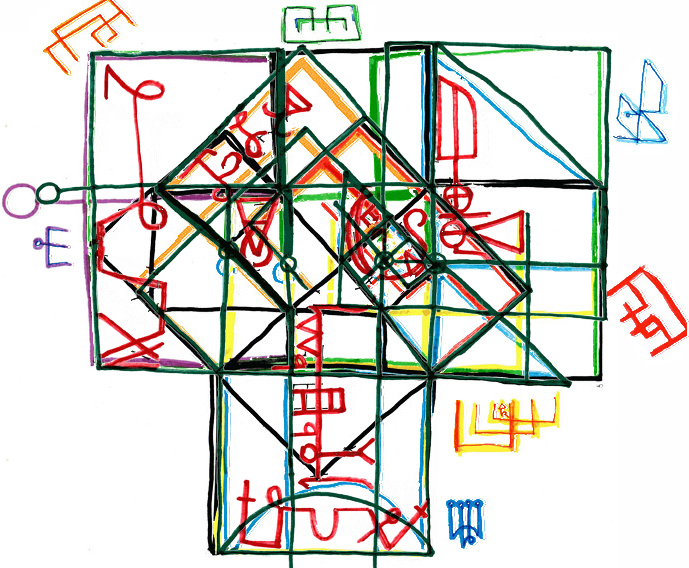
Below is an even clearer outline showing the different "positions" of the zodiac in the seven primary colours into which light is divided by a prism, the shape formed of all of their overlaps in dark green, the shape of the unfolding Pythagorean number-square spiral in black, and the linear/curved sigils of the planetary Archangels in dark red. The correspondence between this many pre-existent attributes onto one single newly-discovered geometric lattice model is truly a fortuitous discovery. It implies that the sources for these divided and uncombined forms might have been, at some time now perhaps lost to antiquity, this very model upon which we cuurrently rest our eyes. One can only wonder at what these strange seals and sigils might represent.
In the next section to this tour I will discuss the "subserviant" Hosts of each of the seven Archangels, the Egyptian dekans, the Hebrew Shemhamforash, etc. For now I will leave you with the following extract from the medieval grimoire (book of shadows) of "Pope" Honorius:

For further research into this area: the Grimoire of Armadel
